如图所示为研究电子枪中电子在电场中运动的简化模型示意图。在Oxy平面的ABCD区域内，存在两个场强大小均为E的匀强电场I和II，两电场的边界均是边长为L的正方形，两个匀强电场相距为L。在该区域AB边的中点处由静止释放电子，不计电子所受重力。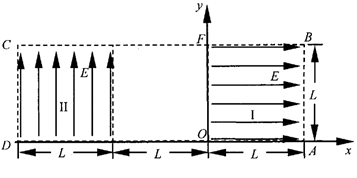
（1）确定电子离开ABCD区域时的位置坐标。
（2）若已知电子电荷量为e、质量为m，求电子由静止释放到离开ABCD区域所经历的时间。
如图甲M、N、P为直角三角形的三个顶点,
,MP中点处固定一电量为Q的正点电荷,MN是长为a的光滑绝缘杆,杆上穿有一带正电的小球（可视为点电荷）,小球自N点由静止释放,小球的重力势能和电势能随位置x（取M点处
）的变化图象如图乙所示，重力加速度为g.设无限远处电势为0，M点所处的水平面为重力零势面。
（1）图乙中表示电势能随位置变化的是哪条图线?
（2）求势能为E1时的横坐标X1和带电小球的质量m;
（3）小球从N点运动到M点时的动能E1
如图所示，P是固定在水平面上的圆弧轨道，O是圆弧的圆心，C为圆弧轨道最高点，D为圆弧轨道最低点。从高台变B点以速度v0水平飞出质量为m、带电量为+q的小球，恰能从圆弧轨道的左端A点沿圆弧切线方向进入，
是OA与竖直方向的夹角。圆弧轨道的竖直直径COD右边存在竖直向下的匀强电场，电场强度为E，已知：m=1kg。V0=3m/s，q=
，
，
，g=10m/s2,sin370=0.6， cos370=0.8.若小球恰能到达最高点C，不计空气阻力和所有摩擦，求：
（1）A、B两点的高度差
（2）圆弧轨道的半径R的大小
在游乐场，有一种大型游乐设施跳楼机，参加游戏的游客被安全带固定在座椅上，提升到离地最大高度60m处，然后由静止释放，开始下落过程可认为自由落体运动，下落2s后受到一恒定阻力而做匀减速运动，且下落到地面速度恰好减为零．已知游客和座椅总质量为2000kg，重力加速度g=10m/s2．求：
（1）下落过程中最大速度
（2）该恒定阻力的大小
如图所示，一半径为R的半圆形光滑轨道固定在竖直平面内。a、b是轨道的两个端点且高度相同，O为圆心。小球A静止在轨道的最低点，小球B从轨道右端b点的正上方距b点高为2R处由静止自由落下，从b点沿圆弧切线进入轨道后，与小球A相碰。第一次碰撞后B球恰返回到b点，A球上升的最高点为c，Oc连线与竖直方向夹角为60°（两球均可视为质点）。求A与B两球的质量之比
。（结果可以用根式表示）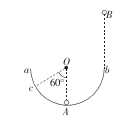
如图所示，足够长的平行玻璃砖厚度d=3
cm，底面镀有反光膜，顶面嵌有涂有遮光物质的挡板AB。一束光线以i=45°的入射角由挡板的A端入射，经底面反射后，恰能从挡板的B端射出。已知光线在玻璃砖中的折射率n=
，真空中的光速c=3×l08
，求：
①光线在玻璃中传播的时间t（不考虑光在玻璃砖上表面的反射）
②挡板AB的长度l