小玲用下面的方法来测量学校教学大楼AB的高度：如图，在水平地面上放一面平面镜，镜子与教学大楼的距离EA=21米．当她与镜子的距离CE=2．5米时，她刚好能从镜子中看到教学大楼的顶端B．已知她的眼睛距地面高度DC=1．6米．请你帮助小玲计算出教学大楼的高度AB是多少米（注意：根据光的反射定律：反射角等于入射角）．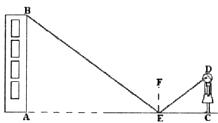
某商场为了“五一”促销，举办抽奖活动，抽奖方案是：将如图的正六边形转盘等分成6个全等三角形，其中两个涂上灰色，顾客任意转动这个转盘2次，当转盘停止时，两次都指向灰色区域的即可获得奖品．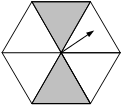
（1）求顾客获得奖品的概率；
（2）商场工作人员又提出了以下几个方案：
①抛掷一枚均匀的硬币3次，3次抛掷的结果都是正面朝上的即可获得奖品；
②一只不透明的袋子中，装有10个白球和20个红球，这些球除颜色外都相同，搅匀后从中任意摸出一个球，记下颜色后放回袋中并搅匀，再从中摸出一个球，两次都摸出白球的即可获得奖品；
③一只不透明的袋子中，装有2个白球和4个红球，这些球除颜色外都相同，搅匀后从中任意摸出两个球，两个都是白球的即可获得奖品；
④任意抛掷一枚均匀的骰子两次，两次朝上的点数都是3的倍数的即可获得奖品；
这几种方案中和原方案获奖概率相同的有（填序号）．
解不等式组：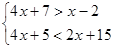
计算：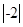
＋（－1）2013－（－2）－2．
如图，抛物线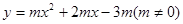
的顶点为H，与
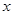轴交于A、B两点（B点在A点右侧），点H、B关于直线：
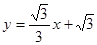对称，过点B作直线BK∥AH交直线于K点．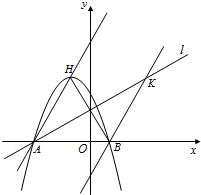 
（1）求A、B两点坐标，并证明点A在直线上；
（2）求此抛物线的解析式；
（3）将此抛物线向上平移，当抛物线经过K点时，设顶点为N，求出NK的长．
如图，△ABC内接于⊙O, AD是⊙O直径, E是CB延长线上一点, 且ÐBAE=ÐC.
（1）求证：直线AE是⊙O的切线；
（2）若EB="AB" ,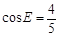 
, AE=24，求EB的长及⊙O的半径。