直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为点E,F.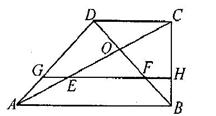
(1)求证:△FOE≌△DOC;
(2)求sin∠OEF的值;
(3)若直线EF与线段AD,BC分别相交于点G,H,求
 的值.
的值.
.何老师在黑板上出了一道题:当x=2010,y=2009时,[2x(x2y-xy2)+xy(2xy-x2)]÷x2y的值.题目出完后,小玉同学说:“老师给的条件y=2009是多余的.”小丹同学说:“不给这个条件就不能求出结果,所以不是多余的.”你认为她们谁说的有道理?为什么?
已知y-1与x成正比例,且当x=-1时,y=3.
(1)求y与x的函数解析式;
(2)当y=-7时,求x的值.
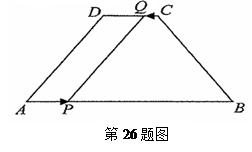
(本题8分)如图,在梯形ABCD中,AB∥DC,AB=14cm,CD=6cm.点P从点A出发,以2cm/s的速度沿AB向终点B运动;点Q从点C出发,以1cm/s的速度沿CD向终点D运动(P、Q两点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒。
(1)当DQ=AP时,四边形APQD是平形四边形,求出此时t的值;
(2) 试问在这样的运动过程中,是否存在某一时刻,使梯形PBCQ的面积是梯形ABCD面积的一半?若存在,求出这样的t的值,若不存在,请说明理由。
 |
(本题6分) 如图,四边形ABCD为矩形,对角线AC、BD相交于点O,CE平行于DB,交AB的延长线于E,试说明AC=CE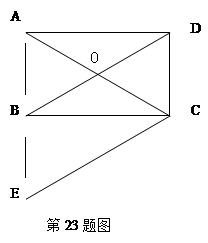
(本题6分)如图,在平行四边形ABCD中,点E是BC边上的一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=56°求∠D的度数.
解: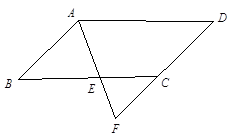
|