如图（a）所示，间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上。在区域I内有方向垂直于斜面的匀强磁场，磁感应强度恒为B不变；在区域Ⅱ内有垂直于斜面向下的匀强磁场，其磁感应强度Bt的大小随时间t变化的规律如图（b）所示。t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑，同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放。在ab棒运动到区域Ⅱ的下边界EF之前，cd棒始终静止不动，两棒均与导轨接触良好。
已知cd棒的质量为m、电阻为R，ab棒的质量、阻值均未知，区域Ⅱ沿斜面的长度为l，在t=tx时刻（tx未知）ab棒恰好进入区域Ⅱ，重力加速度为g。求：
区域I内磁场的方向；
通过cd棒中的电流大小和方向；
ab棒开始下滑的位置离区域Ⅱ上边界的距离；
ab棒开始下滑至EF的过程中，回路中产生总的热量。
（结果用B、l、θ、m、R、g表示）
一机枪每分钟发射600发子弹，每发子弹的质量为 10 g ，发射时速度沿水平方向为 80 m/s。发射子弹时用肩抵住枪托，求枪托对肩水平方向的平均作用力是多少？
高台滑雪运动员经过一段滑行后从斜坡上O点水平飞出，斜坡与水平面的夹角θ=37°，运动员连同滑雪板的总质量m=50kg，他落到了斜坡上的A点，A点与O点的距离s=12m，如图所示。忽略斜坡的摩擦和空气阻力的影响，重力加速度g=10m/s2。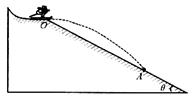
(sin37°=0.60;cos37°=0.80)
（1）运动员在空中飞行了多长时间？
（2）求运动员离开O点时的速度大小。
（3）运动员落到斜坡上顺势屈腿以缓冲，使他垂直于斜坡的速度在t=0.50s的时间内减小为零，设缓冲阶段斜坡对运动员的弹力可以看作恒力，求此弹力的大小。
“神舟”六号载人飞船在空中环绕地球做匀速圆周运动，某次经过赤道的正上空P点时，对应的经线为西经157.5°线，飞船绕地球转一圈后，又经过赤道的正上空P点，此时对应的经线为经度180°．已知地球半径为R，地球表面的重力加速度为g，地球自转的周期为T0．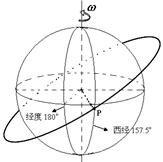
（1）求载人飞船的运动周期；
（2）求飞船运行的圆周轨道离地面高度h的表达式．（用T0、g和R表示）．
小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动。当球某次运动到最低点时，绳恰好断掉，球飞行水平距离d后落地。如图所示。已知握绳的手离地面高度为d，手与球之间的绳长为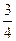
d,重力加速度为g。忽略手的运动半径和空气阻力，绳能承受的最大拉力为定值。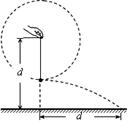
（1）求绳断开时小球的速度；
（2）求绳能承受的最大拉力多大；
（3）若手的位置始终不变，改变绳长使手与球间的绳长变为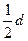
，要使绳仍在球运动到最低点时恰好断掉，求小球飞行的水平距离。
如图，将一根光滑的细金属棒折成V形，顶角为2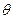
，其对称轴竖直，在其中一边套上一个质量为m的小金属环P，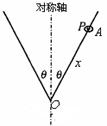
（1）若固定V形细金属棒，小金属环P从距离顶点O为 x的A点处由静止自由滑下，则小金属环由静止下滑至顶点O点时需多少时间？
（2）若小金属环P随V形细金属棒绕其对称轴以角速度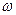
匀速转动时，小金属环与棒保持相对静止，则小金属环离对称轴的距离为多少？