如图所示,电阻忽略不计的、两根两平行的光滑金属导轨竖直放置,其上端接一阻值为3Ω的定值电阻R。在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B,磁场区域的高度为d=0.5m。导体棒a的质量ma=0.2kg、电阻Ra=3Ω;导体棒b的质量mb=0.1kg、电阻Rb=6Ω,它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动,都能匀速穿过磁场区域,且当b 刚穿出磁场时a正好进入磁场.设重力加速度为g=10m/s2,不计a、b棒之间的相互作用。导体棒始终与导轨垂直且与导轨接触良好。求: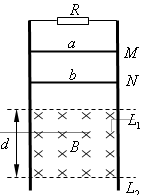
在整个过程中,a、b两棒分别克服安培力所做的功;
导体棒a从图中M处到进入磁场的时间;
M点和N点距L1的高度。
【2015·上海·33】如图,在场强大小为E、水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动。杆的两端分别固定两电荷量均为q的小球A、B;A带正电,B带负电;A、B两球到转轴O的距离分别为2l、l,所受重力大小均为电场力大小的 倍,开始时杆与电场夹角为
倍,开始时杆与电场夹角为 (
( )。将杆从初始位置由静止释放,以O点为重力势能和电势能零点。求:
)。将杆从初始位置由静止释放,以O点为重力势能和电势能零点。求:
(1)初始状态的电势能 ;
;
(2)杆在平衡位置时与电场间的夹角 ;
;
(3)杆在电势能为零处的角速度 。
。
【2015·山东·24】如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径。两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场。间距为d的两平行金属极板间有一匀强电场,上极板开有一小孔。一质量为m,电量为+q的粒子由小孔下方d/2处静止释放,加速后粒子以竖直向上的速度v射出电场,由点紧靠大圆内侧射入磁场。不计粒子的重力。
(1)求极板间电场强度的大小;
(2)若粒子运动轨迹与小圆相切,求区磁感应强度的大小;
(3)若Ⅰ区,Ⅱ区磁感应强度的大小分别为2mv/qD,4mv/qD,粒子运动一段时间后再次经过H点,求这段时间粒子运动的路程。
【2015·上海·32】如图(a)两相距L=0.5m的平行金属导轨固定于水平面上,导轨左端与阻值R=2Ω的电阻连接,导轨间虚线右侧存在垂直导轨平面的匀强磁场,质量m=0.2kg的金属杆垂直于导轨上,与导轨接触良好,导轨与金属杆的电阻可忽略,杆在水平向右的恒定拉力作用下由静止开始运动,并始终与导轨垂直,其v-t图像如图(b)所示,在15s时撤去拉力,同时使磁场随时间变化,从而保持杆中电流为0,求:
(1)金属杆所受拉力的大小为F;
(2)0-15s匀强磁场的磁感应强度大小为 ;
;
(3)15-20s内磁感应强度随时间的变化规律。
【2015·浙江·25】使用回旋加速器的实验需要把离子束从加速器中引出,离子束引出的方法有磁屏蔽通道法和静电偏转法等。质量为m,速度为v的离子在回旋加速器内旋转,旋转轨道时半径为r的圆,圆心在O点,轨道在垂直纸面向外的匀强磁场中,磁感应强度为B。为引出离子束,使用磁屏蔽通道法设计引出器。引出器原理如图所示,一堆圆弧形金属板组成弧形引出通道,通道的圆心位于 点(
点( 点图中未画出)。引出离子时,令引出通道内磁场的磁感应强度降低,从而使离子从P点进入通道,沿通道中心线从Q点射出。已知OQ长度为L。OQ与OP的夹角为
点图中未画出)。引出离子时,令引出通道内磁场的磁感应强度降低,从而使离子从P点进入通道,沿通道中心线从Q点射出。已知OQ长度为L。OQ与OP的夹角为 ,
,
(1)求离子的电荷量q并判断其正负;
(2)离子从P点进入,Q点射出,通道内匀强磁场的磁感应强度应降为 ,求
,求 ;
;
(3)换用静电偏转法引出离子束,维持通道内的原有磁感应强度B不变,在内外金属板间加直流电压,两板间产生径向电场,忽略边缘效应。为使离子仍从P点进入,Q点射出,求通道内引出轨迹处电场强度E的方向和大小。
【2015·北京·22】如图所示,足够长的平行光滑金属导轨水平放置,宽度L=0.4m一端连接R=1 的电阻。导线所在空间存在竖直向下的匀强磁场,磁感应强度B=1T。导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好,导轨和导体棒的电阻均可忽略不计。在平行于导轨的拉力
的电阻。导线所在空间存在竖直向下的匀强磁场,磁感应强度B=1T。导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好,导轨和导体棒的电阻均可忽略不计。在平行于导轨的拉力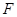 作用下,导体棒沿导轨向右匀速运动,速度v=5m/s。求:
作用下,导体棒沿导轨向右匀速运动,速度v=5m/s。求:
(1)感应电动势E和感应电流I;
(2)在0.1s时间内,拉力的冲量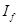 的大小;
的大小;
(3)若将MN换为电阻r=1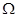 的导体棒,其他条件不变,求导体棒两端的电压U。
的导体棒,其他条件不变,求导体棒两端的电压U。