某同学用位移传感器研究木块在斜面上的滑动情况，装置如图（a）。己知斜面倾角q＝37°。他使木块以初速度v0沿斜面上滑，并同时开始记录数据，绘得木块从开始上滑至最高点，然后又下滑回到出发处过程中的s-t图线如图（b）所示。图中曲线左侧起始端的坐标为（0，1.4），曲线最低点的坐标为（0.6，0.4）。重力加速度g取10m/s2。sin37°＝0.6，cos37°＝0.8求：
木块上滑时的初速度v0和上滑过程中的加速度a1；
木块与斜面间的动摩擦因数m；
木块滑回出发点时的速度vt。
如图所示，半径为R的半球形陶罐，固定在可以绕竖直轴旋转的水平转台上，转台转轴与过陶罐球心O的对称轴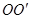
重合，转台以一定角速度
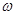匀速旋转，一质量为m的小物块落入陶罐内，经过一段时间后，小物块随陶罐一起转动且相对罐壁静止，它和O点的连线与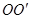之间的夹角
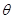为60°。已知重力加速度大小为
，小物块与陶罐之间的最大静摩擦力大小为
。
（1）若小物块受到的摩擦力恰好为零，求此时的角速度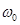
；
（2）若小物块一直相对陶罐静止，求陶罐旋转的角速度的取值范围。
我国志愿者王跃曾与俄罗斯志愿者一起进行“火星-500”的实验活动。假设王跃登陆火星后，测得火星的半径是地球半径的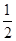
，质量是地球质量的
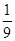。已知地球表面的重力加速度是
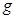，地球的半径为
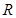，忽略火星以及地球自转的影响，求：
（1）求火星表面的重力加速度g′的大小;
（2）王跃登陆火星后，经测量，发现火星上一昼夜的时间为t，如果要发射一颗火星的同步卫星，它正常运行时距离火星表面将有多远？
海王星有13颗已知的天然卫星。现认为海卫二绕海王星沿圆轨道匀速运转，已知海卫二的质量2.0×l019kg，轨道半径为7.2×106km，运行的周期为360天，万有引力常量G=6.67×l0－1lN·m2/kg2,试估算海王星的质量。（结果保留一位有效数字）
从地面上方某点，将一小球以10m/s 的初速度沿水平方向抛出，小球经过1s落地，不计空气阻力，取g =10m/s²。求小球的位移和落地速度。
起跳摸高是学生常进行的一项活动，小亮同学身高1.72 m，体重60 kg，站立时举手达到2.14 m,他弯曲两腿，再用力蹬地，经0.4 s竖直跳起，设他蹬地的力大小恒为1050N，不计空气阻力，取g="10" m/s２，求小亮同学起跳摸高的最大高度是多少?