（本小题满分6分）如图是4×4方格，其中每个小正方形的边长为1.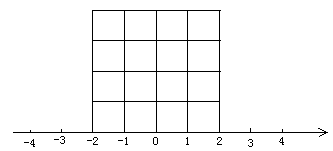
（1）利用
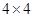的方格，画出面积为5的正方形并涂上阴影；（2）利用（1）的正方形在下面的数轴上表示实数
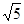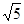和－（保留作图痕迹）。
如图，小明在楼上点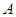
处观察旗杆
，测得旗杆顶部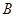
的仰角为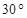
，测得旗杆底部
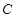的俯角为
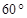，已知点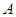距地面的高
为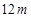
．求旗杆的高度．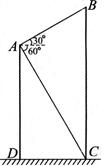
已知抛物线
．
（1）该抛物线和
轴的交点坐标是 ▲ ，顶点坐标是 ▲ ；
（2）选取适当的数据填入下表，并在如图的直角坐标系内描点画出该抛物线的图象；
（3）若该抛物线上两点
的横坐标满足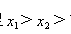
，试比较
与
的大小．
本市某中学的一个数学兴趣小组在本校学生中开展主题为“交通安全知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，划分等级后的数据整理如下表：
| 等级 |
非常了解 |
比较了解 |
基本了解 |
不太了解 |
| 频数 |
40 |
120 |
36 |
4 |
| 频率 |
0．2 |
m |
0．18 |
0．02 |
（1）本次问卷调查取样的样本容量为___▲____，表中的
值为_▲______．
（2）根据表中的数据计算等级为“非常了解”的频数在扇形统计图所对应的扇形的圆心角的度数，并补全扇形统计图．
（3）若该校有学生
人，请根据调查结果估计这些学生中“比较了解”交通安全知识的人数约为多少？
将如图所示的牌面数字分别是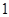
，
，
，
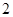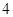的四张扑克牌背面朝上，洗匀后放在桌面上．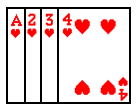
（1）从中随机抽出一张牌，牌面数字是奇数的概率是 ▲；
（2）先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再随机抽取一张，将牌面数字作为个位上的数字，请用画树状图或列表的方法求组成的两位数恰好是的倍数的概率．
先化简，再求值：
其中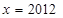
．