(本小题满分12分)设平面α∥β,两条异面直线AC和BD分别在平面α、β内,线段AB、CD中点分别为M、N,设MN=a,线段AC=BD=2a,求异面直线AC和BD所成的角.
(本小题满分13分)已知函数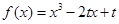 (t∈R) .
(t∈R) .
(Ⅰ)若曲线 在
在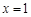 处的切线与直线
处的切线与直线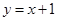 平行,求实数
平行,求实数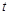 的值;
的值;
(Ⅱ)若对任意的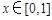 ,
,  恒成立,求实数
恒成立,求实数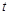 的取值范围.
的取值范围.
已知数列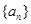 为等比数列,其前
为等比数列,其前 项和为
项和为 ,已知
,已知 ,且对于任意的
,且对于任意的 有
有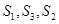 成等差数列;
成等差数列;
(Ⅰ)求数列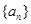 的通项公式;
的通项公式;
(Ⅱ)已知 (
( ),求
),求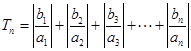 .
.
(本小题共12分)“一站到底”是某电视台推出的大型游戏益智节目.某校高三年级为了解学生暑假期间的收视情况,从高中A,B层6个班共抽取了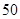 名学生,对他们累计收视时间进行统计,得到如下数据.
名学生,对他们累计收视时间进行统计,得到如下数据.
| 年级 |
人数 |
| A一班 |
4 |
| A二班 |
4 |
| A三班 |
6 |
| B四班 |
12 |
| B五班 |
6 |
| B六班 |
18 |
| 合计 |
50 |

请根据下面的各班人数统计表和收视时间的频率分布直方图解决下列问题:
(Ⅰ)抽查的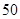 人中,累计收视时间为
人中,累计收视时间为 ~
~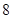 小时的人数有多少?
小时的人数有多少?
(Ⅱ)经调查,累计收视时间不少于 小时的学生均来自B层班.现采用分层抽样的方法,从累计收视时间不少于
小时的学生均来自B层班.现采用分层抽样的方法,从累计收视时间不少于 小时的学生中随机抽取
小时的学生中随机抽取 名学生进行问卷调查,求这三个班级各抽取了多少名学生;
名学生进行问卷调查,求这三个班级各抽取了多少名学生;
(Ⅲ)在(Ⅱ)抽取的 名学生中随机选取
名学生中随机选取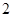 人进行访谈,求这
人进行访谈,求这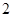 名学生来自不同班级的概率.
名学生来自不同班级的概率.
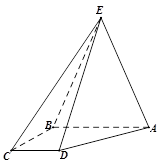
(本小题满分12分)如图,四棱锥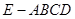 中,
中, ,
,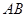 ∥
∥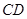 ,
, ,
, .
.
(1)求证: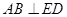 ;
;
(2)线段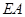 上若存在点
上若存在点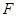 ,满足
,满足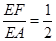 ,求证:
,求证: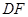 // 平面
// 平面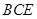 .
.
已知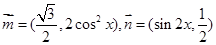 ,
,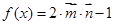 .
.
(I)求函数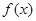 的单调递增区间;
的单调递增区间;
(II)函数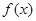 的图象可以由函数
的图象可以由函数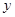
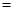
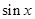 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?