已知直线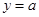 与曲线
与曲线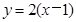 和
和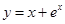 的交点分别为
的交点分别为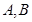 ,则线段
,则线段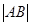 的最小值为________.
的最小值为________.
某天,甲要去银行办理储蓄业务,已知银行的营业时间为9: 00至17:00,设甲在当天13:00至18:00之间任何时间去银行的可能性相同,那么甲去银行恰好能办理业务的概率是.
如图,己知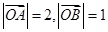 ,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点,
,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点,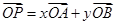 ,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,满足题设条件的为 (写出所有正确式子的序号).
,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,满足题设条件的为 (写出所有正确式子的序号).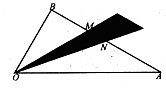
①x≥0,y≥0;②x-y≥0;③x-y≤0;④x-2y≥0;⑤2x-y≥0.
如图,在四棱锥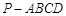 中,底面
中,底面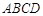 是平行四边形,点
是平行四边形,点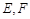 为
为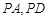 的中点,则面
的中点,则面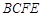 将四棱锥
将四棱锥 所分成的上下两部分的体积的比值为 .
所分成的上下两部分的体积的比值为 .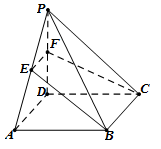
函数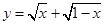 的最大值是______________
的最大值是______________