在平面直角坐标系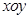 中,经过点
中,经过点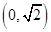 且斜率为
且斜率为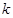 的直线
的直线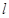 与椭圆
与椭圆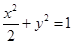 有两个不同的交点
有两个不同的交点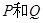 .
.
(1)求实数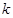 的取值范围;
的取值范围;
(2)设椭圆与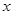 轴正半轴,
轴正半轴,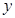 轴正半轴的交点分别为
轴正半轴的交点分别为 ,是否存在常数
,是否存在常数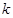 ,使得向量
,使得向量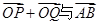 共线?如果存在,求
共线?如果存在,求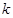 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(本小题满分12分)某公园计划建造一个室内面积为800m2的矩形花卉温室.在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道。沿前侧内墙保留3m宽的空地,中间矩形内种植花卉.当矩形温室的边长各为多少时,花卉的种植面积最大?最大种植面积是多少?
(本小题满分12分)在△ABC中,BC= ,AC=3,sinC=2sinA.
,AC=3,sinC=2sinA.
(Ⅰ)求边长AB的值;
(Ⅱ)求△ABC的面积.
(本小题满分10分)给定两个命题,p:对任意实数x都有 +ax+1>0恒成立;
+ax+1>0恒成立;
q:函数y= (a>0且a≠1)为增函数,若p假q真,求实数a的取值范围.
(a>0且a≠1)为增函数,若p假q真,求实数a的取值范围.
(本小题满分14分)
已知函数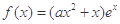 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.
(1)当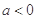 时,解不等式
时,解不等式 ;
;
(2)当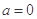 时,求正整数k的值,使方程
时,求正整数k的值,使方程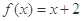 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求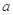 的取值范围.
的取值范围.
(本小题满分13分)
在数列 中,已知
中,已知 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求证:数列 是等差数列;
是等差数列;
(Ⅲ)设数列 满足
满足 ,求
,求 的前n项和
的前n项和 .
.