(本小题满分14分)
已知函数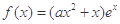 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.
(1)当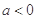 时,解不等式
时,解不等式 ;
;
(2)当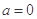 时,求正整数k的值,使方程
时,求正整数k的值,使方程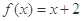 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求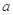 的取值范围.
的取值范围.
设 均为锐角,且
均为锐角,且 .求证:
.求证: .
.
设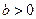 ,椭圆方程为
,椭圆方程为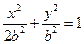 ,抛物线方程为
,抛物线方程为 .如图所示,过点
.如图所示,过点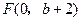 作
作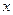 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为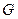 ,已知抛物线在点
,已知抛物线在点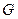 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点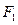 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设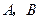 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点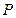 ,使得
,使得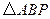 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).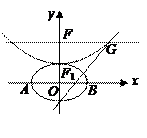
正四棱锥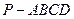 中,
中,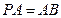 ,
,
点M,N分别在PA,BD上,且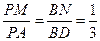 .
.
(Ⅰ)求异面直线MN与AD所成角;
(Ⅱ)求证: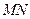 ∥平面PBC;
∥平面PBC;
(Ⅲ)求MN与平面PAB所成角的正弦值.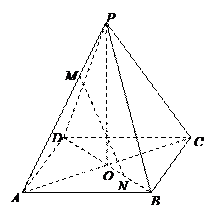
将一枚骰子(形状为正方体,六个面上分别标有数字1,2,3,4,5,6的玩具)先后抛掷两次,骰子向上的点数依次为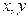 .
.
(1)求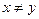 的概率;
的概率;
(2)求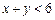 的概率P;
的概率P;
(3)试将右侧求⑵中概率P的伪代码补充完整
已知抛物线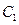 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线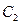 :
: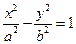 的一个焦点
的一个焦点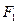 且垂直于
且垂直于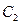 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线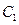 与双曲线
与双曲线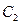 的一个交点是
的一个交点是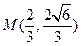 .
.
(1)求抛物线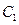 的方程及其焦点
的方程及其焦点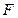 的坐标;
的坐标;
(2)求双曲线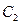 的方程及其离心率
的方程及其离心率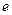 .
.