将一枚骰子(形状为正方体,六个面上分别标有数字1,2,3,4,5,6的玩具)先后抛掷两次,骰子向上的点数依次为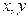 .
.
(1)求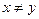 的概率;
的概率;
(2)求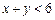 的概率P;
的概率P;
(3)试将右侧求⑵中概率P的伪代码补充完整
其底面ABCD为正方形,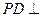 平面
平面 ,
,
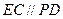 ,且
,且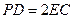 ,
, 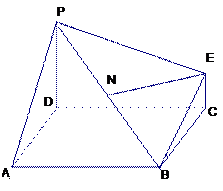
(1)求证: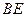 //平面
//平面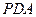 ;
;
(2)若N为线段 的中点,求证:
的中点,求证: 平面
平面 ;
;
设 是满足不等式
是满足不等式 ≥
≥ 的自然数
的自然数 的个数.
的个数.
(1)求 的函数解析式;
的函数解析式;
(2) ,求
,求 ;
;
(3)设 ,由(2)中
,由(2)中 及
及 构成函数
构成函数 ,
, ,求
,求 的最小值与最大值.
的最小值与最大值.
 个正数排成
个正数排成 行
行 列:
列:




其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知 ,
, ,
, ,试求
,试求 的值.
的值.
设数列 的前
的前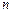 项和为
项和为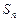 ,
,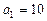 ,
,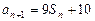 .
.
⑴求证:数列 是等差数列.
是等差数列.
⑵设 是数列
是数列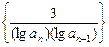 的前
的前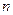 项和,求使
项和,求使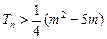 对所有的
对所有的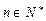 都成立的最大正整数
都成立的最大正整数 的值.
的值.
在△ABC中,已知角A、B、C所对的边分别是a、b、c,边c=,且tanA+tanB=tanA·tanB-,又△ABC的面积为S△ABC=,求a+b的值。