已知抛物线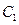 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线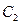 :
: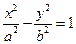 的一个焦点
的一个焦点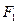 且垂直于
且垂直于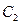 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线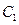 与双曲线
与双曲线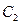 的一个交点是
的一个交点是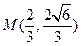 .
.
(1)求抛物线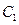 的方程及其焦点
的方程及其焦点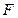 的坐标;
的坐标;
(2)求双曲线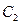 的方程及其离心率
的方程及其离心率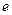 .
.
已知双曲线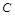 :
: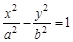
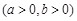 的焦距为
的焦距为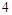 ,以原点为圆心,实半轴长为半径的圆和直线
,以原点为圆心,实半轴长为半径的圆和直线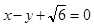 相切.
相切.
(1)求双曲线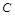 的方程;
的方程;
(2)设点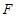 为双曲线
为双曲线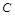 的左焦点,试问在
的左焦点,试问在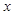 轴上是否存在一定点
轴上是否存在一定点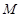 ,过点
,过点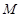 任意作一直线
任意作一直线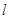 与双曲线
与双曲线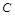 交于
交于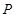 ,
,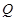 两点,使得
两点,使得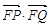 为定值?若存在,求出此定值及点
为定值?若存在,求出此定值及点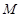 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,在直三棱柱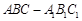 中,
中,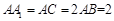 ,且
,且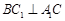 .
.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)设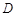 是
是 的中点,判断并证明在线段
的中点,判断并证明在线段 上是否存在点
上是否存在点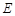 ,使
,使 ‖平面
‖平面 ;若存在,求三棱锥
;若存在,求三棱锥 的体积.
的体积.
某市对该市小微企业资金短缺情况统计如下表:
| 小微企业短缺 资金额(万元) |
[0,20) |
[20,40) |
[40,60) |
[60,80) |
[80,100] |
| 频率 |
0.05 |
0.1 |
0.35 |
0.3 |
0.2 |
(1)试估计该市小微企业资金缺额的平均值;
(2)某银行为更好的支持小微企业健康发展,从其第一批注资的A行业3家小微企业和B行业的2家小微企业中随机选取3家小微企业,进行跟踪调研.求选取的3家小微企业中A行业的小微企业至少有2家的概率.
已知△ABC的三个内角A、B、C的对边分别为a、b、c,且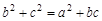 .
.
求:(1)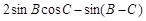 的值;
的值;
(2)若a=2,求△ABC周长的最大值.
已知关于x的不等式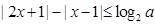 (其中
(其中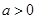 )。
)。
(1)当a=4时,求不等式的解集;
(2)若不等式有解,求实数a的取值范围。