已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球 个。若从袋子中随机抽取1个小球,取到标号为2的小球的概率为
个。若从袋子中随机抽取1个小球,取到标号为2的小球的概率为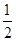 。
。
(1)求 的值;
的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球的标号为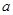 ,第二次取出的小球的标号为
,第二次取出的小球的标号为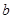 。
。
①记“ ”为事件
”为事件 ,求事件
,求事件 的概率;
的概率;
②在区间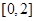 内任取2个实数
内任取2个实数 ,求时间“
,求时间“ 恒成立”的概率.
恒成立”的概率.
(本小题满分13分)设圆C满足:(1)截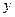 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被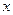 轴分成两段圆弧,其弧长的比为5∶1.在满足条件(1).(2)的所有圆中,求圆心到直线
轴分成两段圆弧,其弧长的比为5∶1.在满足条件(1).(2)的所有圆中,求圆心到直线
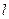 :3
:3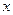 -4
-4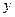 =0的距离最小的圆的方程.
=0的距离最小的圆的方程.
(本小题满分13分)已知函数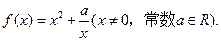
(Ⅰ)当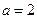 时,解不等式
时,解不等式 >
> ;
;
(Ⅱ)讨论函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
已知△ABC的角A.B.C所对的边分别是a.b.c,设向量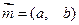 ,
,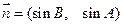 ,
,
(1)若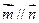 ,求证△ABC为等腰三角形;
,求证△ABC为等腰三角形;
(2)若 ,边长
,边长 ,角
,角 ,求△ABC的面积.
,求△ABC的面积.
(本小题共13分)
已知 函数
函数 .
.
(1)当a=3时,求f(x)的零点;
(2)求函数y=f (x)在区间[1,2]上的最小值.
(本小题共14分)
已知二次函数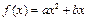 ,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
(1)求f(x)的解析式;
(2)若函 数
数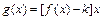 在
在 上是单调减函数,那么:求k的取值范围;
上是单调减函数,那么:求k的取值范围;