(本题满分10分)
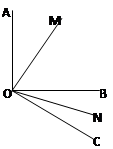
⑴如图,已知∠AOB=90º,∠BOC=30º,OM平分∠AOB,ON平分∠BOC,求∠MON的度数;
⑵如果⑴中∠AOB=α,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
从⑴、⑵的结果中能得出什么结论?
水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克. 经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克。
(1)现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少 元?(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
元?(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
如图,已知一次函数 的图象与
的图象与 轴,
轴, 轴分别相交于A,B两点,点C在AB上以每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用
轴分别相交于A,B两点,点C在AB上以每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用 (单位:秒)表示.
(单位:秒)表示.
(1)求AB的长;
(2)当 为何值时,△ACD与△ABO相似?并直接写出此时点C的坐标.
为何值时,△ACD与△ABO相似?并直接写出此时点C的坐标.
如图,某校九年级(1)班的一个学习小组进行测量小山高度的实践活动,部分同学在 山脚点A测得山腰上一点D的仰角为300,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为450,山腰点D的俯角为600。请你帮助他们计算出小山的高度BC(计算过程和结果都不取近似值)。
山脚点A测得山腰上一点D的仰角为300,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为450,山腰点D的俯角为600。请你帮助他们计算出小山的高度BC(计算过程和结果都不取近似值)。
如图,在直角坐标系中△ABC的A、B、C三点坐标为A(7,1)、B(8,2)、C(9,0).
(1) 请在图中画出△ABC的以点P (12,0)为位似中心,且与△ABC的相似比为3的位似图形△A/B/C/(要求与△ABC同在P点一侧);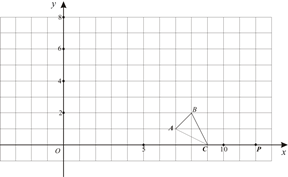
(2)求线段BC的对应线段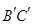 所在直线的解析式.
所在直线的解析式.
某中学七年级有8个班,要从中选出2个班代表学校参加某项活动。七(1)班必须参加,另外再从七(2)至七(8)班选出1个班.七(5)班有学生建议用如下的方法:从装有四个标有数字1、2、3、4的球袋中摸出1个球,记下数字,放回摇匀后再摸出1个球(球的大小、形状与质量完全一样),两次摸出的球上的数字和是几,就选几班。(1)分别求出选七(2)、七(5)、七(8)班的概率;(2)你认为这种方法公平吗?如不公平,请你设计一个公平的方案