如图，在平面直角坐标系中，矩形OABC的顶点A（0，3），C（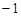
，0）．将矩形OABC绕原点顺时针旋转90°，得到矩形
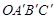．设直线
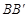与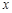
轴交于点M、与
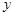轴交于点N，抛物线
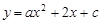的图象经过点C、M、N．解答下列问题：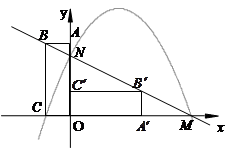
（1）分别求出直线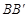和抛物线所表示的函数解析式；
（2）将△MON沿直线MN翻折，点O落在点P处，请你判断点P是否在抛物线上，说明理由．
（3）将直线MN向上平移，使它与抛物线只有一个交点，求此时直线的解析式．
（4）点P是x轴上方的抛物线上的一动点，连接P M，P N ，设所得△PMN的面积为S．
①求S的取值范围；
②若△PMN的面积S为整数，则这样的△PBC共有 个．
．
．
)2＋|－3|；