(本小题满分16分)已知函数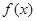 的图象在
的图象在 上连续不断,定义:
上连续不断,定义: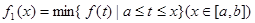 ,
,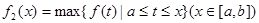
其中,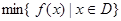 表示函数
表示函数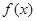 在区间上的最小值,
在区间上的最小值,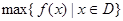 表示函数
表示函数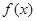 在区间上的最大值.若存在最小正整数
在区间上的最大值.若存在最小正整数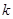 ,使得
,使得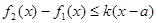 对任意的
对任意的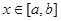 成立,则称函数为区间
成立,则称函数为区间 上的“
上的“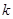 阶收缩函数”.
阶收缩函数”.
(1)若 ,试写出
,试写出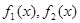 的表达式;
的表达式;
(2)已知函数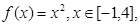 试判断
试判断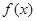 是否为
是否为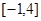 上的“
上的“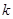 阶收缩函数”,如果是,求出相应的
阶收缩函数”,如果是,求出相应的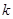 ;如果不是,请说明理由;
;如果不是,请说明理由;
(3)已知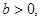 函数
函数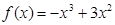 是
是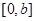 上的2阶收缩函数,求
上的2阶收缩函数,求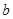 的取值范围.
的取值范围.
(本小题满分7分)选修4—5:不等式选讲
已知正数 满足
满足 ,
,
(Ⅰ)求证: ;(Ⅱ) 求
;(Ⅱ) 求 的最小值.
的最小值.
(本小题满分7分)《选修4-4:坐标系与参数方程》
在直角坐标系xOy中,圆C的参数方程 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆C的交点为O,P,与直线
与圆C的交点为O,P,与直线 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
(本小题满分7分)选修4—2:矩阵与变换
若二阶矩阵 满足
满足 .
.
(Ⅰ)求二阶矩阵 ;
;
(Ⅱ)把矩阵 所对应的变换作用在曲线
所对应的变换作用在曲线 上,求所得曲线的方程.
上,求所得曲线的方程.
(本小题满分14分)已知函数 (其中
(其中 ,e是自然对数的底数,e=2.71828…).
,e是自然对数的底数,e=2.71828…).
(Ⅰ)当 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)若 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅲ)求证:对任意正整数n,都有 .
.
在平面直线坐标系XOY中,给定两点A(1,0),B(0,-2),点C满足 ,其中
,其中 ,且
,且 .
.
(1)求点C的轨迹方程.
(2)设点C的轨迹与双曲线 (
( )相交于M,N两点,且以MN为直径的圆经过原点,求证:
)相交于M,N两点,且以MN为直径的圆经过原点,求证: 是定值.
是定值.
(3)在(2)条件下,若双曲线的离心率不大于 ,求该双曲线实轴的取值范围.
,求该双曲线实轴的取值范围.