(本小题满分14分)如图,在直三棱柱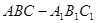 中,
中, ,
,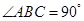 ,
, 是
是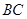 的中点.
的中点.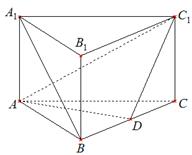
(Ⅰ)求证: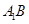 ∥平面
∥平面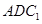 ;
;
(Ⅱ)求二面角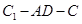 的余弦值;
的余弦值;
(Ⅲ)试问线段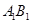 上是否存在点
上是否存在点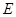 ,使
,使 与
与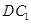 成
成 角?若存在,确定
角?若存在,确定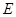 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.
(本题12分)某商业集团对所属的200家连锁店进行评估,并依据得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,评估标准如下表:
| 评估得分 |
[60,70) |
[70,80) |
[80,90) |
[90,100) |
| 评定类型 |
D |
C |
B |
A |
现将各连锁店的评估分数进行统计分析,并将其画成频率分布直方图如下.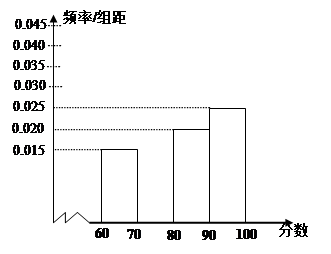
(1)请补全频率分布直方图(画出[70,80)那组对应的小长方形并标上对应高度)
(2)现欲用分层抽样的方法从这200家连锁店中抽取40家作为代表进行座谈会,试问其中A、D类连锁店分别应抽取多少家?
(3)试根据频率分布直方图估计这200家连锁店评估得分的中位数(结果保留一位小数).
(本小题满分13分)已知函数
(Ⅰ)讨论函数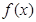 的单调性;
的单调性;
(Ⅱ)设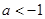 .如果对任意
.如果对任意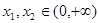 ,
, ,求
,求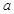 的取值范围.
的取值范围.
(本小题满分13分)已知椭圆
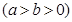 的离心率为
的离心率为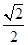 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(Ⅰ)求椭圆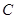 的方程;
的方程;
(Ⅱ)若过点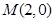 的直线与椭圆
的直线与椭圆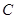 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足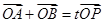 (其中
(其中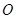 为坐标原点),求整数
为坐标原点),求整数 的最大值.
的最大值.
(本小题满分13分)提高过江大桥的车辆通行能力可改善整个城市的交通状况。在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数。当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当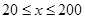 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(Ⅰ)当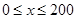 时,求函数
时,求函数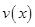 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)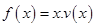 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)
(本小题满分12分)已知等差数列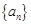 满足:
满足: ,
,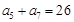 .
.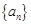 的前n项和为
的前n项和为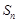 .
.
(Ⅰ)求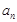 及
及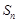 ;
;
(Ⅱ)令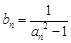 (
(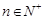 ),求数列
),求数列 的前
的前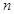 项和
项和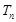 .
.