如图甲所示，水平加速电场的加速电压为U0，在它的右侧有由水平正对放置的平行金属板a、b构成的偏转电场，已知偏转电场的板长L="0.10" m，板间距离d=5.0×10-2 m，两板间
接有如图15乙所示的随时间变化的电压U，且a板
电势高于b板电势。在金属板右侧存在有界的匀强磁场，磁场的左边界为与金属板右侧重合的竖直平面MN，MN右侧的磁场范围足够大，磁感应强度B=5.0×10-3T，方向与偏转电场正交向里（垂直纸面向里）。质量和电荷量都相同的带正电的粒子从静止开始经过电压U0=50V的加速电场后，连续沿两金属板间的中线OO′方向射入偏转电场中，中线OO′与磁场边界MN垂直。已知带电粒子的比荷
=1.0×108 C/kg，不计粒子所受的重力和粒子间的相互作用力，忽略偏转电场两板间电场的边缘效应，在每个粒子通过偏转电场区域的极短时间内，偏转电场可视作恒定不变。
求t=0时刻射入偏转电场的粒子在磁场边界上的入射点和出射点间的距离；
求粒子进入磁场时的最大速度；
对于所有进入磁场中的粒子，如果要增大粒子在磁场边界上的入射点和出射点间的距离，应该采取哪些措施？试从理论上推理说明。
所谓“水流星”表演时，就是用绳系着装有水的小桶，在竖直平面内做圆周运动，而水不洒落。如果在表演“水流星”节目时，栓杯子的绳长为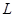
，其最大承受力是杯子和杯内水的重量的8倍，要使绳子不断裂，节目表演成功，杯子通过最高点时速度的取值范围为多少？
如图甲所示，一质量为m＝1 kg的物块静止在粗糙水平面上的A点，从t＝0时刻开始，物块在按如图乙所示规律变化的水平力F的作用下向右运动，第3 s末物块运动到B点且速度刚好为0，第5 s末物块刚好回到A点，已知物块与粗糙水平面间的动摩擦因数μ＝0.2，g取10 m/s2，求：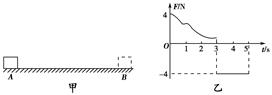
A、B间的距离；
水平力F在5 s时间内对物块所做的功．
有一质量为m的航天器靠近地球表面绕地球作圆周运动（轨道半径等于地球半径），某时刻航天器启动发动机，在很短的时间内动能变为原来的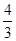
，此后轨道为椭圆，远地点与近地点距地心的距离之比是2：1，经过远地点和经过近地点的速度之比为 1：2．己知地球半径为R，地球质量为M，万有引力恒量为G．求航天器靠近地球表面绕地球作圆周运动时的动能；
在从近地点运动到远地点的过程中克服地球引力所做的功为多少?
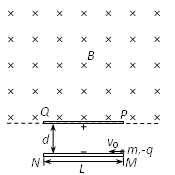
如图所示，MN、PQ是平行金属板，板长为L，两板间距离为d，在PQ板的上方有垂直纸面向里的匀强磁场。一个电荷量为q、质量为m的带负电粒子以速度v0从MN板边缘沿平行于板的方向射入两板间，结果粒子恰好从PQ板左边缘飞进磁场，然后又恰好从PQ板的右边缘飞进电场。不计粒子重力。试求：两金属板间所加电压U的大小；
匀强磁场的磁感应强度B的大小；
在图中画出粒子再次进入电场的运动轨迹，并标出粒子再次从电场中飞出的位置与速度方向。
如图所示的电路中，电源的电动势E=12V，内阻未知，R1=8Ω，R2=1.5Ω，L为规格“3V，3W”的灯泡，开关S断开时，灯泡恰好正常发光。（不考虑温度对灯泡电阻的影响）试求：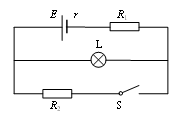
灯泡的额定电流和和灯丝电阻；
电源的内阻；
开关S闭合时，灯泡实际消耗的功率。