.
点A、B分别是椭圆 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于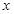 轴上方,
轴上方,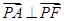 .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于 ,求点M的坐标;
,求点M的坐标;
(3)在(2)的条件下,求椭圆上的点到点M的距离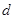 的最小值.
的最小值.
(本小题满分12分)
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).某校高一·一班50名学生在上学期参加活动的次数统计如条形图所示.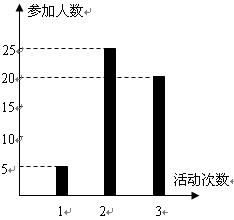
(Ⅰ)求该班学生参加活动的人均次数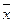 ;
;
(Ⅱ)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率;
(Ⅲ)从该班中任选两名学生,用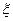 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量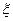 的分布列及数学期望
的分布列及数学期望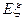 .(要求:答案用最简分数表示)
.(要求:答案用最简分数表示)
(本小题满分12分)在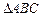 中,
中,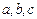 分别为角
分别为角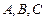 的对边,且满足
的对边,且满足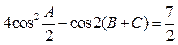
(Ⅰ)求角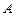 的大小;
的大小;
(Ⅱ)若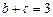 ,求
,求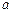 的最小值.
的最小值.
曲线C上任一点到点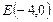 ,
,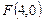 的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方,
的距离的和为12,C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方, .
.
(Ⅰ)求曲线C的方程;
(Ⅱ)求点P的坐标;
(Ⅲ)以曲线C的中心为圆心,AB为直径作圆O,过点P的直线l截圆O的弦MN长为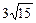 ,求直线l的方程.
,求直线l的方程.
若函数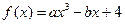 ,当
,当 时,函数
时,函数 有极值为
有极值为 ,
,
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 有3个解,求实数
有3个解,求实数 的取值范围。
的取值范围。
设函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求函数 的最大值和最小值.
的最大值和最小值.