为备战2012年伦敦奥运会,爾家篮球队分轮次迸行分项冬训.训练分为甲、乙两组,根据经验,在冬训期间甲、乙两组完成各项训练任务的概率分别为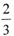 和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
和P(P>0)假设每轮训练中两组都各有两项训练任务需完成,并且每项任务的完成与否互不影响.若在一轮冬训中,两组完成训练任务的项数相等且都不小于一项,则称甲、乙两组为“友好组”
(I)若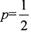 求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
求甲、乙两组在完成一轮冬训中成为“友好组”的概率;
(II)设在6轮冬训中,甲、乙两组成为“友好组”的次数为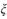 ,当
,当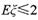 时,求P的取值范围.
时,求P的取值范围.
(本小题13分)
盒子里有6张大小相同的卡片,上面分别写着1,2,3,4,5,6这6个数.
⑴现从盒子中任取两张卡片,求两张卡片上的数字之和为偶数的概率;
⑵现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶数的卡片则停止抽取,否则继续进行,求抽取次数为多少时其概率小于 .
.
(本小题13分)
在△ 中,
中, .
.
⑴求 的值;
的值;
⑵若△ 的面积为
的面积为 ,
, ,求
,求 的长.
的长.
(本小题12分)
已知数列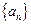 满足:
满足: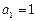 ,
,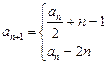
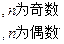 ,记
,记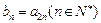 ,
,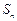 为数列
为数列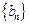 的前
的前 项和.
项和.
⑴证明数列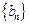 为等比数列,并求其通项公式;
为等比数列,并求其通项公式;
⑵若对任意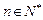 且
且 ,不等式
,不等式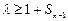 恒成立,求实数
恒成立,求实数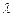 的取值范围;
的取值范围;
⑶令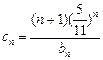 ,证明:
,证明: .
.
(本小题12分)
设椭圆 右焦点为
右焦点为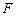 ,它与直线
,它与直线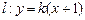 相交于
相交于 、
、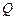 两点,
两点,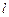 与
与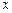 轴的交点
轴的交点 到椭圆左准线的距离为
到椭圆左准线的距离为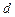 ,若椭圆的焦距
,若椭圆的焦距 是
是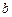 与
与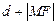 的等差中项.
的等差中项.
⑴求椭圆离心率 ;
;
⑵设点 与点
与点 关于原点
关于原点 对称,若以
对称,若以 为圆心,
为圆心,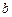 为半径的圆与
为半径的圆与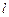 相切,且
相切,且 求椭圆
求椭圆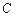 的方程.
的方程.
已知曲线 在点
在点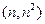 处的切线方程为
处的切线方程为 ,其中
,其中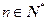
(1)求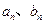 关于
关于 的表达式;
的表达式;
(2)设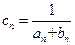 ,求证:
,求证: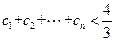 ;
;
(3)设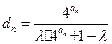 ,其中
,其中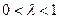 ,求证:
,求证: