古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )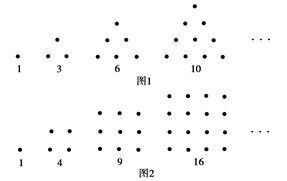
| A.289 | B.1024 | C.1225 | D.1378 |
函数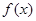 的定义域为开区间
的定义域为开区间 ,导函数
,导函数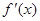 在
在 内的图象如图所示,则函数
内的图象如图所示,则函数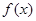 在开区间
在开区间 内有极小值点()
内有极小值点()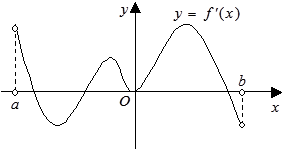
| A.4个 | B.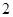 个 个 |
C.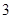 个 个 |
D.1个 |
已知F1,F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是正三角形,则这个椭圆的离心率是( )
A. |
B.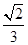 |
C. |
D. |
函数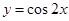 在点
在点 处的切线方程是( )
处的切线方程是( )
A.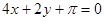 |
B.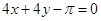 |
C.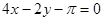 |
D.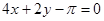 |
在正方体ABCD-A1B1C1D1中,M、N分别为棱AA1和BB1的中点,则sin〈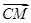 ,
,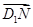 〉的值为( )
〉的值为( )
A. |
B.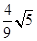 |
C.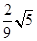 |
D.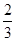 |