、学习正切函数ytanx后，数学哥赵文峰同学在自己的数学葵花-优题课

、学习正切函数y=tanx后，“数学哥”赵文峰同学在自己的“数学葵花宝典”中，对其性质做了系统梳理：
①正切函数是周期函数，最小正周期是π
②正切函数是奇函数
③正切函数的值域是实数集R，在定义域内无最大值和最小值
④正切函数在开区间（，），内都是增函数，不能说在整
个定义域内是增函数；正切函数不会在某一个区间内是减函数。
⑤与正切曲线不相交的直线是，
⑥正切曲线是中心对称图形，其对称中心坐标是，
以上论断中正确的有（）

A．3个

B．4个

C．5个

D．6个

科目数学题型选择题难度容易

知识点：多面角及多面角的性质

青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据 L和小数记录表的数据 V的满足 $L = 5 + \lg V$ ．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据为（）（ $\sqrt[10]{10} \approx 1.259$ ）

1.5

1.2

0.8

0.6

已知 $(1 - i)^{2} z = 3 + 2 i$ ，则 $z =$ （）

A．

$- 1 - \frac{3}{2} i$

B．

$- 1 + \frac{3}{2} i$

C．

$- \frac{3}{2} + i$

D．

$- \frac{3}{2} - i$

为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：

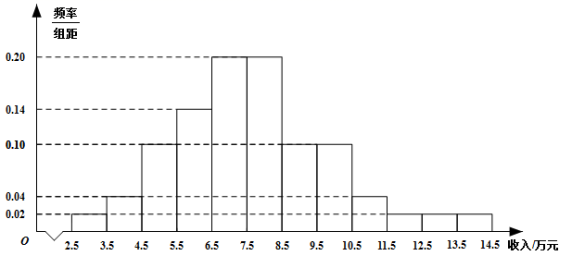
根据此频率分布直方图，下面结论中不正确的是（）

A．	该地农户家庭年收入低于4.5万元的农户比率估计为6%
B．	该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C．	估计该地农户家庭年收入的平均值不超过6.5万元
D．	估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间

设集合 $M = \{x |0 < x < 4\}, N = \{x |\frac{1}{3} \leq x \leq 5\}$ ，则 $M \cap N =$ （）

A．	$\{x \|0 < x \leq \frac{1}{3}\}$	B．	$\{x \|\frac{1}{3} \leq x < 4\}$
C．	$\{x \|4 \leq x < 5\}$	D．	$\{x \|0 < x \leq 5\}$

设 $a \in R$ , 函数 $f （ x ） = \{\begin{matrix} \cos (2 πx - 2 πa), & x < a, \\ x^{2} - 2 (a + 1) x + a^{2} + 5, & x ⩾ a \end{matrix}$ 若函数 $f (x)$ 在区间 $(0, + \infty)$ 内恰有 6 个零点, 则（）

A．	$(2, \frac{9}{4}] \cup (\frac{5}{2}, \frac{11}{4}]$	B．	$(\frac{7}{4}, 2] \cup (\frac{5}{2}, \frac{11}{4}]$
C．	$(2, \frac{9}{4}] \cup [\frac{11}{4}, 3)$	D．	$[\frac{7}{4}, 2) \cup [\frac{11}{4}, 3)$