(本题8分)某商店需要购进一批电视机和洗衣机，根据市场调查，决定电视机进货量不少于洗衣机的进货量的一半．电视机与洗衣机的进价和售价如下表：
计
划购进电视机和洗衣机共100台，商店最多可筹集资金160 800元．（1）请你帮助商店算一算有多少种进货方案？（不考虑除进价之外的其它费用）
（2）哪种进货方案待商店销售购进的电视机与洗衣机完毕后
获得利润最多？并求出最多利润．（利润＝售价－进价）
如图，已知点I是△ABC的内心，AI交BC于D，交外接圆O于E，求证：
（1）IE=EC；
（2）IE2=ED•EA．
已知，如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．
（1）以AB边上一点O为圆心，过A，D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由；
（2）若（1）中的⊙O与AB边的另一个交点为E，AB=6，BD=
，求⊙O的半径．
在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．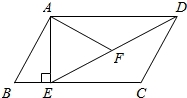
（1）求证：△ADF∽△DEC；
（2）若AB=4，AD=3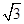
，AE=3，求AF的长．
某商店准备进一批季节性小家电，每个进价为40元，经市场预测，销售定价为50元，可售出400个；定价每增加1元，销售量将减少10个．设每个定价增加x元．
（1）写出售出一个可获得的利润是 元．（用含x的代数式表示）
（2）商店若准备获得利润6000元，并且使进货量较少，则每个定价为多少元？
如图，AB是⊙O的直径，BC是⊙O的弦，半径OD⊥BC，垂足为E，若BC=
，DE=3．
求：
（1）⊙O的半径；
（2）弦AC的长；
（3）阴影部分的面积．