某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个定价增加x元.
(1)写出售出一个可获得的利润是 元.(用含x的代数式表示)
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?
一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
(1)请你根据上述统计数据,把下面的图和表补充完整;
一分钟投篮成绩统计分析表:
(2)下面是小明和小聪的一段对话,请你根据(1)中的表,写出两条支持小聪的观点的理由。
如图1,某超市从一楼到二楼的电梯AB的长为16.50米,坡角∠BAC为32°。
(1)求一楼于二楼之间的高度BC(精确到0.01米);
(2)电梯每级的水平级宽均是0.25米,如图2.小明跨上电梯时,该电梯以每秒上升2级的高度运行,10秒后他上升了多少米(精确到0.01米)?备用数据:sin32°=0.5299,con32°=0.8480,tan32°=6249。
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
(1)计算: ;(2)解不等式组:
;(2)解不等式组: 。
。
如图,把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中,使直角边OB、OD在x轴上.已知点A(1,2),过A、C两点的直线分别交x轴、y轴于点E、F.抛物线y=ax2+bx+c经过O、A、C三点.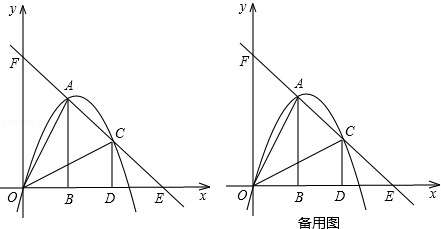
(1)求该抛物线的函数解析式;
(2)点P为线段OC上一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM为等腰梯形?若存在,求出此时点P的坐标;若不存在,请说明理由.
(3)若△AOB沿AC方向平移(点A始终在线段AC上,且不与点C重合),△AOB在平移过程中与△COD重叠部分面积记为S.试探究S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.