((本题14分)如图4,已知椭圆 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4
,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线PF1、PF2的斜率分别为 ;
;
(Ⅲ)是否存在常数 ,使得
,使得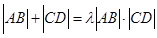 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
某地区有100户农民,都从事水产养殖。据了解,平均每户的年收入为3万元。为了调整产业结构,当地政府决定动员部分农民从事水产加工。据估计,如果能动员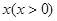 户农民从事水产加工,那么剩下的继续从事水产养殖的农民平均每户的年收入有望提高
户农民从事水产加工,那么剩下的继续从事水产养殖的农民平均每户的年收入有望提高 ,而从事水产加工的农民平均每户的年收入将为
,而从事水产加工的农民平均每户的年收入将为 万元.
万元.
(1)在动员 户农民从事水产加工后,要使从事水产养殖的农民的总年收入不低于动员前从事水产养殖的农民的总年收入,求
户农民从事水产加工后,要使从事水产养殖的农民的总年收入不低于动员前从事水产养殖的农民的总年收入,求 的取值范围;
的取值范围;
(2)若 ,要使这100户农民中从事水产加工的农民的总年收入始终不高于从事水产养殖的农民的总年收入,求
,要使这100户农民中从事水产加工的农民的总年收入始终不高于从事水产养殖的农民的总年收入,求 的最大值.
的最大值.
(1)过点P(-1,-2)的直线 分别交x轴和y轴的负半轴于A、B两点,当|PA|·|PB|最小时,求
分别交x轴和y轴的负半轴于A、B两点,当|PA|·|PB|最小时,求 的方程.
的方程.
(2)已知定点 与定直线
与定直线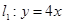 ,过
,过  点的直线
点的直线 与
与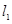 交于第一象限
交于第一象限 点,与x轴正半轴交于点
点,与x轴正半轴交于点 ,求使
,求使 面积最小的直线
面积最小的直线 方程。
方程。
直线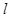 通过点P(1,3)且与两坐标轴的正半轴交于A、B两点.
通过点P(1,3)且与两坐标轴的正半轴交于A、B两点.
(1)直线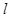 与两坐标轴所围成的三角形面积为6,求直线
与两坐标轴所围成的三角形面积为6,求直线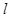 的方程;
的方程;
(2)求 的最小值;
的最小值;
(3)求 的最小值.
的最小值.
在△ABC中,角A,B,C所对的边分别为a,b,c.若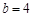 ,
, .
.
(1)求 的值;
的值;
(2)求函数 的值域.
的值域.
已知三条直线l1:x+y+1=0,l2:2x-y+8=0,l3:a x+3y-5=0 .分别求下列各题中a的值:(1)三条直线相交于一点;(2)三条直线只有两个不同的交点;(3)三条直线有三个不同的交点.