通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表：
性别与看营养说明列联表 单位: 名
| |
男 |
女 |
总计 |
| 看营养说明 |
50 |
30 |
80 |
| 不看营养说明 |
10 |
20 |
30 |
| 总计 |
60 |
50 |
110 |
（I）从这50名女生中按是否看营养说明采取分层抽样，抽取一个容量为
的样本，问样本中看与不看营养说明的女生各有多少名?
(Ⅱ) 从（I）中的5名女生样本中随机选取两名作深度访谈, 求选到看与不看营养说明的女生各一名的概率；
（III）根据以上列联表，问有多大把握认为“性别与在购买食物时看营养说明”有关？
如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，
总计耗用9．6米铁丝，再用
平方米塑料片制成圆柱的侧面和下底面（不安装上底面）。
（Ⅰ）当圆柱底面半径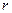
取何
值时，取得最大值？并求出该最大值（结果精确到0．01平方米）；
（Ⅱ）若要制作一个如图放置的，底面半径为0．3米的灯笼，请作出用于灯笼的三视图（作图时，不需考虑骨架等因素）。
平面EFGH分别平行空间四边形ABCD中的CD与AB且交BD、AD、
AC、BC于E、F、G、H．CD=a,AB=b,CD⊥AB．
（1）求证EFGH为矩形；
（2）点E在什么位置，SEFGH最大?
在平面α内有△ABC，在平面α外有点S，斜线SA⊥AC，SB⊥BC,且
斜线SA、SB与平面α所成角相等。
（1）求证：AC=BC
（2）又设点S到α的距离为4cm,AC⊥BC且AB=6cm,求S与AB的距离。
已知椭圆
的离心率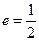
，且椭圆过点
.
(1)求椭圆
的方程；
(2)若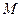
为椭圆上的动点,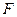
为椭圆的右焦点,以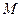为圆心,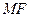
长为半径作圆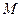,过点
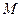作圆的两条切线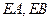
,（
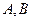为切点），求点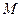的坐标，使得四边形
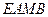的面积最大．]