(. (本小题满分12分)已知函数
(Ⅰ)若函数 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(Ⅱ)设 求证:
求证: .
.
(本小题满分12分)袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求:
(Ⅰ)取出的3个小球上的数字互不相同的概率;
(Ⅱ)随机变量 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)计分介于20分到40分之间的概率
(本小题满分10分)在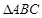 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是 ,已知向量
,已知向量 ,
, ,且
,且 。
。
(Ⅰ)求角A的大小;
(Ⅱ)若 ,求
,求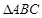 面积的最大值。
面积的最大值。
设函数 .
.
(1)解不等式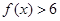 ;
;
(2)若关于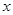 的不等式
的不等式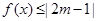 的解集不是空集,试求实数
的解集不是空集,试求实数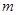 的取值范围.
的取值范围.
已知圆锥曲线C:
 为参数)和定点
为参数)和定点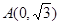 ,
,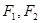 是此圆锥曲线的左、右焦点。
是此圆锥曲线的左、右焦点。
(1)以原点O为极点,以x轴的正半轴为极轴建立极坐标系,求直线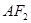 的极坐标方程;
的极坐标方程;
(2)经过点 ,且与直线
,且与直线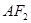 垂直的直线
垂直的直线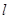 交此圆锥曲线于
交此圆锥曲线于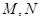 两点,求
两点,求 的值.
的值.
如图, 是圆的两条平行弦,
是圆的两条平行弦, ,
, 交
交 于
于 、交圆于
、交圆于 ,过
,过 点的切线交
点的切线交 的延长线于
的延长线于 ,
,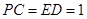 ,
, .
.
(1)求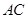 的长;
的长;
(2)求证: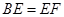 .
.