(本小题满分14分)
已知函数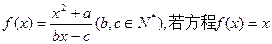 有且只有两个相异实根0,2,且
有且只有两个相异实根0,2,且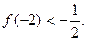
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)已知各项均不为1的数列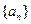 满足
满足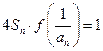 ,求通
,求通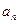 ,
,
(Ⅲ)设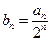 ,求数列
,求数列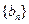 的前
的前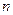 项和
项和 .
.
如图6,在平面直角坐标系 中,设点
中,设点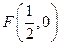 ,直线
,直线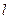 :
: ,点
,点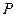 在直线
在直线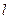 上移动,
上移动,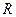 是线段
是线段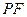 与
与 轴的交点,
轴的交点, 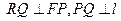 .
.
(I)求动点 的轨迹的方程
的轨迹的方程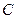 ;
;
(II)设圆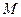 过
过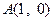 ,且圆心
,且圆心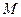 在曲线
在曲线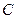 上,
上, 是圆
是圆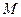 在
在 轴上截得的弦,当
轴上截得的弦,当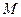 运动时弦长
运动时弦长 是否为定值?请说明理由.
是否为定值?请说明理由.
(本小题满分14分)
如图4,四棱锥P-ABCD的底面ABCD是正方形,PD垂直于底面ABCD,已知四棱锥的正视图,如图5所示,
(Ⅰ)若M是PC的中点,证明:DM⊥平面PBC;
(Ⅱ)求棱锥A-BDM的体积. 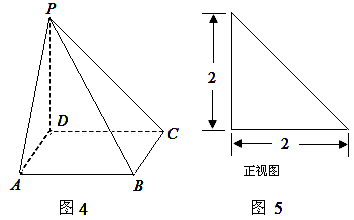
(本小题满分12分)
第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行,为了搞好接待工作,组委会决定对礼仪小姐进行培训.已知礼仪小姐培训班的项目A与项目B成绩抽样统计表如下,抽出礼仪小姐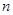 人,成绩只有
人,成绩只有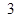 、
、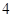 、
、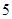 三种分值,设
三种分值,设 分别表示项目A与项目B成绩.例如:表中项目A成绩为
分别表示项目A与项目B成绩.例如:表中项目A成绩为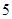 分的共7+9+4=20人.已知
分的共7+9+4=20人.已知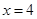 且
且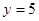 的概率是
的概率是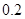 .
.
(I)求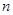 ;
;
(II)若在该样本中,再按项目B的成绩分层抽样抽出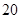 名礼仪小姐,则
名礼仪小姐,则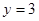 的礼仪小姐中应抽多少人?
的礼仪小姐中应抽多少人?
(Ⅲ)已知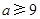 ,
,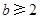 ,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率.
,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率.
(本小题满分14分)已知函数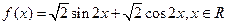 .
.
(I)求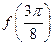 的值;
的值;
(II)求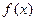 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅲ)若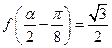 ,
,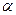 是第二象限的角,求
是第二象限的角,求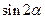 .
.