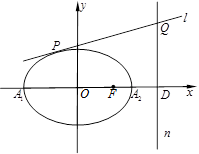
如图,已知椭圆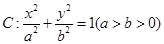 的离心率是
的离心率是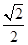 ,
, 分别是椭圆
分别是椭圆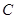 的左、右两个顶点,点
的左、右两个顶点,点 是椭圆
是椭圆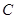 的右焦点。点
的右焦点。点 是
是 轴上位于
轴上位于 右侧的一点,且满足
右侧的一点,且满足 .
.
(1)求椭圆 的方程以及点
的方程以及点 的坐标;
的坐标;
(2)过点 作
作 轴的垂线
轴的垂线 ,再作直线
,再作直线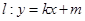 与椭圆
与椭圆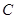 有且仅有一个公共点
有且仅有一个公共点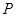 ,直线
,直线 交直线
交直线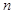 于点
于点 .求证:以线段
.求证:以线段 为直径的圆恒过定点,并求出定点的坐标.
为直径的圆恒过定点,并求出定点的坐标.
(本小题满分14分)
已知数列 满足
满足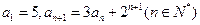 ;
;
(1)证明:数列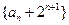 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(2)若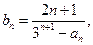 求数列
求数列 的前
的前 项和为
项和为 ;
;
(3)令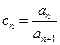 ,数列
,数列 的前
的前 项和为
项和为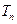 ,求证:
,求证: .
.
(本小题满分13分)
已知点 是函数
是函数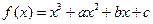 的图像上的两点,若对于任意实数
的图像上的两点,若对于任意实数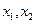 ,当
,当 时,以
时,以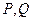 为切点分别作函数
为切点分别作函数 的图像的切线,则两切线必平行,并且当
的图像的切线,则两切线必平行,并且当 时函数
时函数 取得极小值1.
取得极小值1.
(1)求函数 的解析式;
的解析式;
(2)若 是函数
是函数 的图像上的一点,过
的图像上的一点,过 作函数
作函数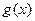 图像的切线,切线与
图像的切线,切线与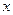 轴和直线
轴和直线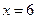 分别交于
分别交于 两点,直线
两点,直线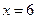 与
与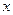 轴交于
轴交于 点,求△ABC的面积的最大值.
点,求△ABC的面积的最大值.
(本小题满分12分)如图,已知圆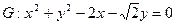 经过椭圆
经过椭圆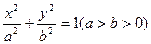 的右焦点F及上顶点B.过点
的右焦点F及上顶点B.过点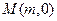 作倾斜角为
作倾斜角为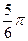 的直线
的直线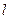 交椭圆于C、D两点.
交椭圆于C、D两点.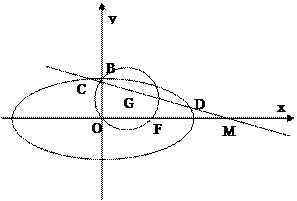
(1)求椭圆的方程;
(2)若点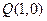 恰在以线段CD为直径
恰在以线段CD为直径
的圆的内 部,求实数
部,求实数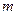 范围.
范围.
( 本小题满分12分)
本小题满分12分)
某公司为了实现2011年10 00万元利润的目标,准备制定一个激励销售人员的奖励方案:
00万元利润的目标,准备制定一个激励销售人员的奖励方案:
销售利润达到10万元时,按销售利润进行奖励,且奖金数额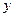 (单位:万元)随销售利润
(单位:万元)随销售利润 (单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的
(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的 ,现有三个奖励模型:
,现有三个奖励模型: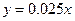 ,
,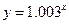 ,
, ,问其中是否有模型能完全符合公司的要求?说明理由.(参考数据:
,问其中是否有模型能完全符合公司的要求?说明理由.(参考数据: )
)
(本小题满分12分)
已知矩形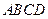 的对角线交于点
的对角线交于点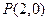 ,边
,边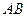 所在直线的方程为
所在直线的方程为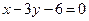 ,点
,点 在边
在边 所在的直线上,
所在的直线上,
(1)求矩形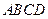 的外接圆的方程;
的外接圆的方程;
(2)已知直线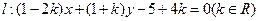 ,求证:直线
,求证:直线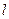 与矩形
与矩形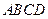 的外接圆恒相交,并求出相交的弦长最短时的直线
的外接圆恒相交,并求出相交的弦长最短时的直线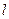 的方程.
的方程.