(本题满分12分)如图,已知椭圆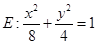 焦点为
焦点为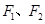 ,双曲线
,双曲线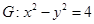 ,设
,设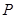 是双曲线
是双曲线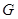 上
上 异于顶点的任一点,直线
异于顶点的任一点,直线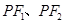 与椭圆的交点分别为
与椭圆的交点分别为 和
和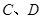 。
。
1. 设直线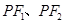 的斜率分别为
的斜率分别为 和
和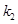 ,求
,求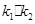 的值;
的值;
2. 是否存在常数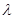 ,使得
,使得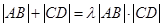 恒成立?若存在,试求出
恒成立?若存在,试求出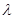 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
3. 
已知等差数列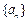 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列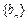 的首项为b,公比为a,其中a,b都是大于1的正整数,且
的首项为b,公比为a,其中a,b都是大于1的正整数,且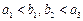 .
.
(1)求a的值;
(2)若对于任意的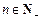 ,总存在
,总存在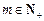 ,使得
,使得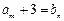 成立,求b的值;
成立,求b的值;
(3)令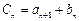 ,问数列
,问数列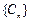 中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
抛物线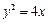 的焦点为F,
的焦点为F,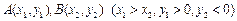 在抛物线上,且存在实数λ,使
在抛物线上,且存在实数λ,使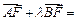 0,
0,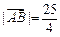 .
.
(1)求直线AB的方程;
(2)求△AOB的外接圆的方程.
已知
是公差为
的等差数列,
是公比为
的等比数列。
(1)若
,是否存在
,有
?请说明理由;
(2)若
(
为常数,且
)对任意
存在
,有
,试求
满足的充要条件;
(3)若
试确定所有的
,使数列
中存在某个连续
项的和式数列中
的一项,请证明。
已知双曲线
的中心是原点,右焦点为
,一条渐近线
,设过点
的直线
的方向向量
.
(1)求双曲线
的方程;
(2)若过原点的直线
,且
与
的距离为
,求
的值;
(3)证明:当
时,在双曲线
的右支上不存在点
,使之到直线
的距离为
.
定义:对于函数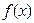 ,
,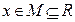 .若
.若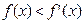 对定义域内的
对定义域内的 恒成立,则称函数
恒成立,则称函数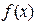 为
为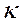 函数.(1)请举出一个定义域为
函数.(1)请举出一个定义域为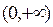 的
的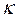 函数,并说明理由;(2)对于定义域为
函数,并说明理由;(2)对于定义域为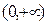 的
的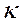 函数
函数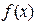 ,求证:对于定义域内的任意正数
,求证:对于定义域内的任意正数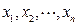 ,均有
,均有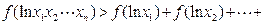
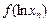 ;
;
(3)对于值域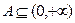 的
的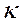 函数
函数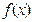 ,求证:
,求证: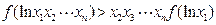 .
.