如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为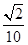 、
、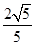 .求:
.求: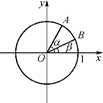
(1) tan(α+β)的值;
(2) α+2β的值.
已知函数f(x)=lnx-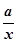 .
.
(1)当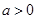 时,判断f(x)在定义域上的单调性;
时,判断f(x)在定义域上的单调性;
(2)若f(x)在[1,e]上的最小值为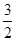 ,求
,求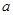 的值.
的值.
求证:.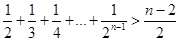
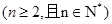 .
.
已知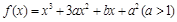 在
在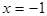 时有极值0。
时有极值0。
(1)求常数 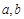 的值;
的值;
(2)求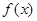 的单调区间。
的单调区间。
(3)方程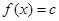 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数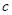 的范围。
的范围。
三个女生和五个男生排成一排.
(1)如果女生必须全排在一起,有多少种不同的排法?
(2)如果女生必须全分开,有多少种不同的排法?
(3)如果两端都不能排女生,有多少种不同的排法?
(4)如果两端不能都排女生,有多少种不同的排法?
已知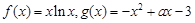 .
.
(1)求函数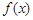 在
在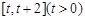 上的最小值;
上的最小值;
(2)对一切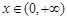 ,
,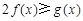 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3) 证明:对一切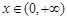 ,都有
,都有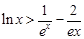 成立.
成立.