三个女生和五个男生排成一排.
(1)如果女生必须全排在一起,有多少种不同的排法?
(2)如果女生必须全分开,有多少种不同的排法?
(3)如果两端都不能排女生,有多少种不同的排法?
(4)如果两端不能都排女生,有多少种不同的排法?
一个四棱锥的三视图如图所示,E为侧棱PC上一动点。
(1)画出该四棱锥的直观图,并指出几何体的主要特征(高、底等).
(2)点 在何处时,
在何处时, 面EBD,并求出此时二面角
面EBD,并求出此时二面角 平面角的余弦值
平面角的余弦值
已知等差数列 满足:
满足: ,
, ,
, 的前n项和为
的前n项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)令bn=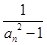 (
( ),求数列
),求数列 的前n项和
的前n项和 。
。
已知向量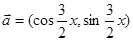 ,
, ,且
,且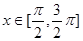
(1)求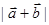 的取值范围;
的取值范围;
(2)求函数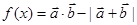 的最小值,并求此时x的值
的最小值,并求此时x的值
设等差数列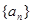 的公差
的公差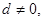 且
且 记
记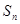 为数列
为数列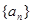 的前
的前 项和.
项和.
(1)若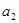 、
、 、
、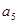 成等比数列,且
成等比数列,且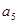 、
、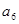 的等差中项为
的等差中项为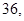 求数列
求数列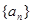 的通项公式;
的通项公式;
(2)若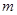 、
、 、
、 且
且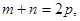 证明:
证明: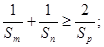
(3)若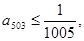 证明:
证明: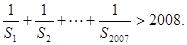
已知函数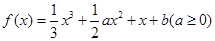 ,
, 为函数
为函数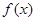 的导函数.
的导函数.
(1)设函数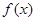 的图象与
的图象与 轴交点为
轴交点为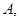 曲线
曲线 在
在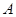 点处的切线方程是
点处的切线方程是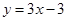 ,求
,求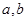 的值;
的值;
(2)若函数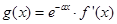 ,求函数
,求函数 的单调区间.
的单调区间.