已知向量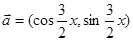 ,
, ,且
,且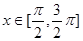
(1)求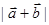 的取值范围;
的取值范围;
(2)求函数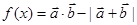 的最小值,并求此时x的值
的最小值,并求此时x的值
已知函数f(x)=|log2(x+1)|,实数m、n在其定义域内,且m<n,f(m)=f(n).
求证:(1)m+n>0;
(2)f(m2)<f(m+n)<f(n2).
某人乘坐出租车从A地到乙地,有两种方案:第一种方案,乘起步价为10元,每km价1.2元的出租车;第二种方案,乘起步价为8元,每km价1.4元的出租车,按出租车管理条例,在起步价内,不同型号的出租车行驶的里路是相等的,则此人从A地到B地选择哪一种方案比较适合?
设 求证
求证
已知等差数列{an}的公差大于0,且a3,a5是方程x2-14x+45=0的两根,数列{bn}的前n项和为Sn,且Sn=1-bn.
(1)求数列{an}、{bn}的通项公式;
(2)记cn=anbn,求证:cn+1≤cn.
已知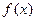 是定义在
是定义在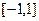 上的奇函数,且
上的奇函数,且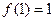 ,若
,若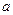 、
、
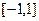 ,
, ,有
,有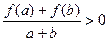 ;
;
(1)判断函数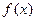 在
在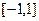 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(2)若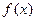 ≤
≤ 对所有的
对所有的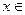
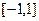 、
、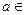
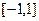 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。