(本题满分14分).如图,圆锥的轴截面SAB为等腰直角三角形,Q为底面圆周上的一点,如果QB的中点为C,OH⊥SC,垂足为H。
求证:BQ⊥平面SOC,
求证:OH⊥平面SBQ;设 ,
, ,求此圆锥的体积。
,求此圆锥的体积。
已知函数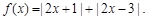
(1)求不等式 的解集;
的解集;
(2)若关于x的不等式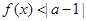 的解集非空,求实数
的解集非空,求实数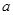 的取值范围.
的取值范围.
选修4—4:坐标系与参数方程
已知直线l: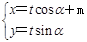 (t为参数)恒经过椭圆C:
(t为参数)恒经过椭圆C: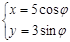 (为参数)的右焦点F.
(为参数)的右焦点F.
(Ⅰ)求m的值;
(Ⅱ)设直线l与椭圆C交于A,B两点,求|FA|·|FB|的最大值与最小值.
选修4-1:几何证明选讲
如图,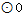 是
是 ABC的外接圆,D是
ABC的外接圆,D是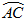 的中点,BD 交AC于E
的中点,BD 交AC于E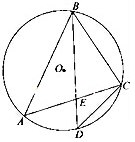
(1)求证: :
:
(2)若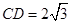 ,O到AC的距离为1,求
,O到AC的距离为1,求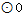 的半径
的半径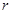
已知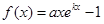 ,
,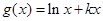
(Ⅰ)当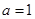 时,若
时,若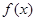 在
在 上为减函数,
上为减函数, 在
在 上是增函数,求
上是增函数,求 值;
值;
(Ⅱ)对任意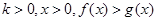 恒成立,求
恒成立,求 的取值范围.
的取值范围.
.已知椭圆C的中心在原点,焦点在x轴上,离心率等于 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点P(2,3), Q(2,-3)在椭圆上,A,B是椭圆上位于直线PQ两恻的动点,
①若直线AB的斜率为 ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足于∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.