如图,已知A、B、C、D均在已知圆上,AD‖BC,CA平分∠BCD,
∠ADC=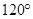 ,四边形ABCD周长为10.
,四边形ABCD周长为10.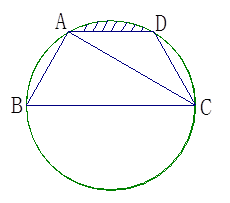
(1)求此圆的半径;
(2)求圆中阴影部分的面积.
(本题6分)如图,已知一次函数 与反比例函数
与反比例函数 的图象交于A、B两点.
的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)观察图象,请直接写出一次函数值小于反比例函数值的 的取值范围.
的取值范围.
(本题6分)如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD= ,坡长AB=
,坡长AB= ,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=
,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F= ,求AF的长度.
,求AF的长度.
(本题6分)计算:
(本题11分)如图,平面直角坐标系中画出了函数l1: 的图象。
的图象。
(1)根据图象,求k,b的值;
(2)请在图中画出函数l2: 的图象;
的图象;
(3)分别过A、B两点作直线l2的垂线,垂足为E、F.
|
问线段AE、BF、EF三者之间的关系,并说明理由.
(4)设l3: ,分别过A、B两点作直线l3的垂线,垂足为E、F.直接写出线段AE、BF、EF三者之间的关系 .
,分别过A、B两点作直线l3的垂线,垂足为E、F.直接写出线段AE、BF、EF三者之间的关系 .
(本题10分)
在向红星镇居民介绍王家庄位置的时候,我们可以这样说:如图,在以红星镇为原点,正东方向为x轴正方向,正北方向为y轴正方向的平面直角坐标系(1单位长度表示的实际距离为1km)中,王家庄的坐标为(5,5);也可以说,王家庄在红星镇东北方向 km的地方。
km的地方。
还有一种方法广泛应用于航海、航空、气象、军事等领域。如右下图:在红星镇所建的雷达站O的雷达显示屏上,把周角每15°分成一份,正东方向为0°,相邻两圆之间的距离为1个单位长度(1单位长度表示的实际距离为1km),现发现2个目标,我们约定用(10,15°)表示点M在雷达显示器上的坐标,则:
(1)点N可表示为;王家庄位置可表示为;点N关于雷达站点0成中心对称的点P的坐标为;
(2)S△OMP=;
(3)若有一家大型超市A在图中(4,30°)的地方,请直接标出点A,并将超市A与雷达站O连接,现准备在雷达站周围建立便民服务店B,使得△ABO为底角30°的等腰三角形,请直接写出B点在雷达显示屏上的坐标.