今年北京市大规模加固中小学校舍,房山某中学教学楼的后面靠近一座山坡,坡面上是一块平地,如图所示.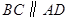 ,斜坡
,斜坡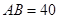 米,坡度i=
米,坡度i=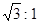 ,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造.经地质人员勘测,当坡角不超过
,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造.经地质人员勘测,当坡角不超过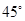 时,可确保山体不滑坡,改造时保持坡脚
时,可确保山体不滑坡,改造时保持坡脚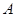 不动,从坡顶
不动,从坡顶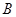 沿
沿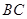 削进到
削进到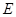 处,问
处,问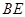 至少是多少米.(结果保留根号)
至少是多少米.(结果保留根号)
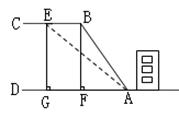
如图,AC和BD相交于点O,OA=OC,OB=OD.求证:DC∥AB.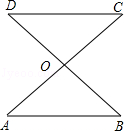
抛物线y=ax2+bx+c与x轴的交点为A(m﹣4,0)和B(m,0),与直线y=﹣x+p相交于点A和点C(2m﹣4,m﹣6).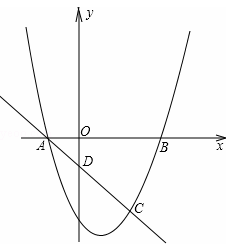
(1)求抛物线的解析式;
(2)若点P在抛物线上,且以点P和A,C以及另一点Q为顶点的平行四边形面积为12,求点P,Q的坐标;
(3)在(2)条件下,若点M是x轴下方抛物线上的动点,当△PQM的面积最大时,请求出△PQM的最大面积及点M的坐标.
如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠ABC=∠CAD.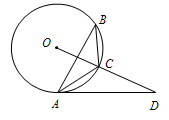
(1)若∠ABC=20°,则∠OCA的度数为;
(2)判断直线AD与⊙O的位置关系,并说明理由;
(3)若OD⊥AB,BC=5,AB=8,求⊙O的半径.
如图,已知直线y=4-x与反比例函数y= (m>0,x>0)的图象交于A、B两点,与x轴、y轴分别相交于C、D两点.
(m>0,x>0)的图象交于A、B两点,与x轴、y轴分别相交于C、D两点.
(1)如果点A的横坐标为1,利用函数图象求关于x的不等式4-x< 的解集;
的解集;
(2)如果点A的横坐标仍然为1,是否存在以AB为直径的圆经过点P(1,0)?若存在,求出m的值;若不存在,请说明理由.
如图,等腰梯形ABCD中,AB=CD,AD∥BC,点E、F在BC上,且BE=CF.
(1)求证:AE=DF;
(2)若AD=EF,试证明四边形AEFD为矩形.