如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA＝3，OC＝2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．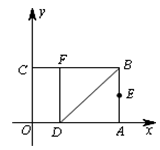
（1）直接写出点E、F的坐标；
（2）设顶点为F的抛物线交y轴正半轴于点P，且以点E、F、P为顶点的三角形是等腰三角形，求该抛物线的解析式；
（3）在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．
初中生的视力状况受到全社会的广泛关注，某市有关部门对全市3万名初中生视力状况进行了一次抽样调查，如图是利用所得数据绘制的频数分布直方图(长方形的高表示该组人数)，根据图中所提供的信息，回答下列问题：
（1）本次调查共抽测了名学生，占该市初中生总数的百分比是；
（2）从左到右五个小组的频率之比是；
（3）如果视力在4.9以上(含4.9)均属正常，则全市有名初中生的视力正常， 视力正常的合格率是．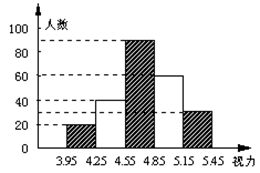
如图，在边长为1个单位长度的小正方形组成的两格中，点A、B、C都是格点．
（1）将△ABC绕点C顺时针旋转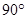
得到△A1B1C1；
（2）作△ABC关于点O成中心对称的△A2B2C2.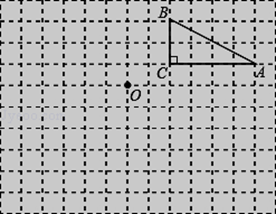
（1）计算：
（2）先化简，再求值
，其中
．
问题情境：如图1，直角三角板ABC中，∠C＝90°，AC＝BC，将一个用足够长的的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上，再将该直角绕点D旋转，并使其两边分别与三角板的AC边、BC边交于P、Q两点。
问题探究：（1）在旋转过程中，
①如图2，当AD＝BD时，线段DP、DQ有何数量关系？并说明理由。
②如图3，当AD＝2BD时，线段DP、DQ有何数量关系？并说明理由。
③根据你对①、②的探究结果，试写出当AD＝nBD时，DP、DQ满足的数量关系为_______________（直接写出结论，不必证明）
（2）当AD＝BD时，若AB＝20，连接PQ，设△DPQ的面积为S，在旋转过程中，S是否存在最小值或最大值？若存在，求出最小值或最大值；若不存在，请说明理由。
图1图2图3
已知抛物线
与x轴交于点
、C，与y轴交于点B（0，3），抛物线的顶点为p。
（1）求抛物线的解析式；
（2）若抛物线向下平移k个单位后经过点（－5，6）。
①求k的值及平移后抛物线所对应函数的最小值；
②设平移后抛物线与y轴交于点D，顶点为Q，点M是平移后的抛物线上的一个动点。请探究：当点M在何处时，△MBD的而积是△MPQ面积的2倍？求出此时点M的坐标。