(1)先化简,再求值: ,其中a=-2,b=3
,其中a=-2,b=3
(2)已知 ,ab=-2,求代数式
,ab=-2,求代数式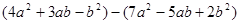 的值.
的值.
因式分解:
(1) ;
;
(2)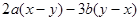 ;
;
(3) ;
;
(4)(x+y)2+2(x+y)+1;
(5)(m2+n2)2-4m2n2;
(6)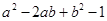
计算:
(1)用乘法公式计算:
(2)1-2(1-2x+ )+3(-
)+3(- +x-1)
+x-1)
(3)-12 ÷(-3
÷(-3 )·(-
)·(- y)
y)
(4)(2a- )(
)( +2a)
+2a)
如图,对称轴为直线x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(-3,0),C为抛物线与y轴的交点且S△ABC=6
(1)求点B的坐标和抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;
(3)①设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值;
②若点M是抛物线上在A、C之间的一个动点,则三角形ACM的最大面积是多少?
已知A=a+2,B=2a2-3a+10,C=a2+5a-3,
(1)求证:无论a为何值,A-B<0成立,并指出A,B的大小关系;
(2)请分析A与C的大小关系.