如图所示，在正方形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场。在t=0时刻，一位于ad边中点o的粒子源在abcd平面内发射出大量的同种带电粒子，所有粒子的
初速度大小相同，方向与od边的夹角分布在0～180°范围内。已知沿od方向发射的粒子在
时刻刚好从磁场边界cd上的p点离开磁场，粒子在磁场中做圆周运动的半径恰好等于正方形边长L，粒子重力不计，求：
（1）粒子的比荷q／m；
（2）假设粒子源发射的粒子在0～180°范围内均匀分布，此时刻仍在磁场中的粒子数与粒子源发射的总粒子数之比；
（3）从粒子发射到全部粒子离开磁场所用的时间。（若角度不特殊时可以用反三角表示，如：已知sinθ＝0.3，则θ＝arcsin0.3)
某电厂要将电能输送到较远的用户, 输送的总功率为9.8×104 W, 电厂输出电压仅为350 V, 为减少输送功率损失, 先用一升压变压器将电压升高再输出. 已知输电线路的总电阻为4 Ω, 允许损失的功率为输送功率的5%, 所需电压为220 V, 求升压、降压变压器的原、副线圈的匝数比各是多少？
如图所示, 理想变压器原线圈中输入电压U1＝3300 V, 副线圈两端电压U2为220 V, 输出端连有完全相同的两个灯泡L1和L2, 绕过铁芯的导线所接的电压表V的示数U＝2 V,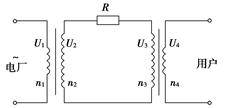 
(1)原线圈n1等于多少匝？
(2)当开关S断开时, 表A2的示数I2＝5 A, 则表A1的示数I1为多少？
(3)当开关S闭合时, 表A1的示数I1′等于多少？
如图所示为一小型交变电流发电机的工作原理图，两磁极间的磁场可看成勻强磁场，磁感应强度为B，矩形线圈abcd以恒定角速度ω绕垂直于磁场方向的固定轴OO’逆时针方向转动，矩形abcd关于OO’对称，已知矩形线圈共有N匝，边长为L1,bc边长为L2，线圈电阻为r，外接电阻为R。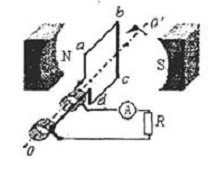
(1) 在线圈位于如图所示的垂直于磁场方向的位置开始计时,规定由a→b(或c→d)方向的感应电动势为正,推导出线圈中感应电动势e随时间t变化的表达式。
(2) 求交流电流表（内阻不计）的读数。
如图所示，直线MN下方无磁场，上方空间存在两个匀强磁场，其分界线是半径为R的半圆，两侧的磁场方向相反且垂直于纸面，磁感应强度大小都为B。现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出，最终打到Q点，不计微粒的重力。求：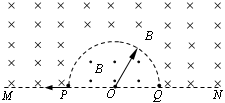
（1）微粒在磁场中运动的周期；
（2）从P点到Q点，微粒的运动速度大小及运动时间；
（3）若向里磁场是有界的，分布在以O点为圆心、半径为R和2R的两半圆之间的区域，上述微粒仍从P点沿半径方向向左侧射出，且微粒仍能到达Q点，求其速度的最大值。
如图（甲）所示的滑轮，它可以绕垂直于纸面的光滑固定水平轴O转动。轮上绕有轻质柔软细线，线的一端系一重物，另一端系一质量为m的金属杆。在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF，在QF之间连接有阻值为R的电阻，其余电阻不计，磁感应强度为B的匀强磁场与导轨平面垂直。开始时金属杆置于导轨下端，将质量为M的重物由静止释放，重物最终能匀速下降。运动过程中金属杆始终与导轨垂直且接触良好，已知重力加速度为g，忽略所有摩擦。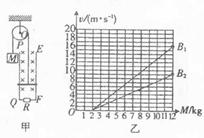
（1）重物匀速下降的速度v的大小是多少？
（2）对一定的磁感应强度B，重物的质量M取不同的值，测出相应的重物做匀速运动时的速度，可得出v-M实验图线。图（乙）中画出了磁感应强度分别为B1和B2时的两条实验图线，试根据实验结果计算B1和B2的比值。
（3）若M从静止到匀速的过程中一共下降的高度为h，求这一过程中R上产生的焦耳热。