(本小题满分13分)已知椭圆 :
: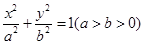 的右焦点为
的右焦点为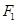
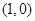 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆 的方程及左顶点
的方程及左顶点 的坐标;
的坐标;
(Ⅱ)设过点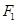 的直线交椭圆
的直线交椭圆 于
于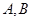 两点,若
两点,若 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程.
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC
(1)求证:BE=2AD;
(2)当AC=3,EC=6时,求AD的长.
设函数 .
.
(1)求 的单调区间和极值;
的单调区间和极值;
(2)若 ,当
,当 时,
时, 在区间
在区间 内存在极值,求整数
内存在极值,求整数 的值.
的值.
已知圆 的圆心在坐标原点
的圆心在坐标原点 ,且恰好与直线
,且恰好与直线 相切,设点A为圆上一动点,
相切,设点A为圆上一动点, 轴于点
轴于点 ,且动点
,且动点 满足
满足 ,设动点
,设动点 的轨迹为曲线
的轨迹为曲线
(1)求曲线C的方程,
(2)直线l与直线l,垂直且与曲线C交于B、D两点,求△OBD面积的最大值.
如图,三棱柱 的侧棱
的侧棱 平面
平面 ,
, 为等边三角形,侧面
为等边三角形,侧面 是正方形,
是正方形, 是
是 的中点,
的中点, 是棱
是棱 上的点.
上的点.
(1)若 是棱
是棱 中点时,求证:
中点时,求证: 平面
平面 ;
;
(2)当 时,求正方形
时,求正方形 的边长.
的边长.
某种产品的广告费支出z与销售额y(单位:万元)之间有如下对应数据:
若广告费支出z与销售额y回归直线方程为多一6.5z+n(n∈R).
(1)试预测当广告费支出为12万元时,销售额是多少?
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.