(本小题满分12分)首届世界低碳经济大会11月17日在南昌召开,本届大会以“节能减排,绿色生态”为主题。某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
(本小题满分12分)在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且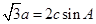 .
.
(1)求角C;
(2)若c=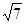 ,且△ABC的面积为
,且△ABC的面积为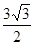
 ,求a+b的值.
,求a+b的值.
(本小题满分12分)某同学用五点法画函数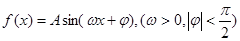 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
 |
0 |
 |
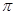 |
 |
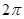 |
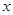 |
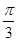 |
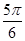 |
|||
 |
0 |
5 |
-5 |
0 |
(1)请将上表数据补充完整,并直接写出函数 的解析式;
的解析式;
(2)若函数 的图像向左平移
的图像向左平移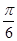 个单位后对应的函数为
个单位后对应的函数为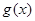 ,求
,求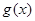 的图像离原点最近的对称中心.
的图像离原点最近的对称中心.
(本小题满分12分)已知向量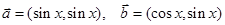 ,若函数
,若函数
(1)求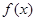 的最小正周期;
的最小正周期;
(2)若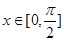 ,求
,求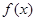 的单调减区间.
的单调减区间.
(本小题满分10分)已知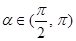 ,且
,且 ,
,
(1)求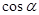 的值;
的值;
(2)若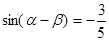 ,
, ,求
,求 的值.
的值.
设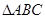 的三个内角
的三个内角 的对边分别是
的对边分别是 ,已知
,已知 ,
,
求角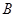 ;
;
若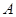 是
是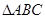 的最大内角,求
的最大内角,求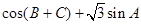 的取值范围.
的取值范围.