在如图所示竖直平面坐标系内，在第四象限内存在垂直纸面向里的匀强磁场和水平方向的匀强电场，磁感应强度为B，电场强度E1的大小和方向未知。质量为
、带电量为q的液滴从p点沿图中虚线匀速运动到原点o进入第二象限，在第二象限内存在水平向右的匀强电场，其场强大小为E2。已知P点坐标为(4L，-3L)，重力加速度为g。求：
E1的方向和大小。
液滴在第四象限匀速运动的速度大小。
液滴通过0点后再次通过
轴时的坐标。
消防车的供水系统主要由水泵、输水管道和水炮组成.如图所示，消防水炮离地高度为
，建筑物上的火点离地高度为
，水炮与火点的水平距离为
，水泵的功率为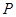
，整个供水系统的效率
.假设水从水炮水平射出，不计空气阻力，取
.
（1）若
,
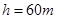，水炮出水速度
，求水炮与起火建筑物之间的水平距离；
（2）在（1）问中，若水炮每秒出水量
，求水泵的功率；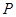
（3）当完成高层灭火后,还需要对散落在火点正下方地面上的燃烧物进行灭火,将水炮竖直下移至
,假设供水系统的效率
不变,水炮出水口的横截面积不变，水泵功率应调整为
，则应为多大？
如图所示，光滑绝缘半球槽的半径为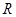
，处在水平向右的匀强电场中，一质量为
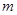的带电小球从槽的右端A处无初速沿轨道滑下，滑到最低位置B时，球对轨道的压力为
.求：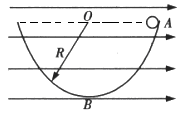
（1）小球受到电场力的大小和方向；（2）带电小球在滑动过程中的最大速度。
如图所示的电场，等势面是一簇互相平行的竖直平面，间隔均为
，各面电势已在图中标出，现有一质量为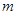
的带电小球以速度
，方向与水平方向成
角斜向上射入电场，要使小球做直线运动．问：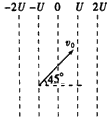
（1）小球应带何种电荷？电荷量是多少？（2）在入射方向上小球最大位移量是多少？(电场足够大)
如图所示，质量均为m的A、B两球，以轻质弹簧连接后置于光滑水平面上，开始弹簧处于自然状态。一质量为
的泥丸P以水平速度v0沿A、B连线向A运动，击中A并粘合在一起，求以后的运动过程中弹簧的最大弹性势能。
如图，一个三棱镜的截面为等腰直角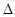
ABC，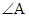
为直角。一细束光线沿此截面所在平面且平行于BC边的方向射到AB边上的M点，M、A间距为l。光进入棱镜后直接射到AC边上，并刚好能发生全反射。试求：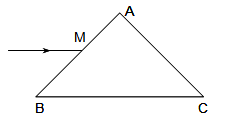
（i）该棱镜材料的折射率n=？
（ii）光从AB边到AC边的传播时间t=？（已知真空中的光速为c。）