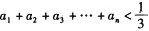.(本小题满分12分)如图所示,矩形ABCD的边AB= ,BC=2,PA⊥平面ABCD,PA=2,现有数据: ①
,BC=2,PA⊥平面ABCD,PA=2,现有数据: ① ;②
;② ;③
;③ ;建立适当的空间直角坐标系,
;建立适当的空间直角坐标系,
(I)当BC边上存在点Q,使PQ⊥QD时, 可能取所给数据中的哪些值?请说明理由;
可能取所给数据中的哪些值?请说明理由;
(II)在满足(I)的条件下,若 取所给数据的最小值
取所给数据的最小值 时,这样的点Q有几个? 若沿BC方向依次记为
时,这样的点Q有几个? 若沿BC方向依次记为 ,试求二面角
,试求二面角 的大小.
的大小.
((本小题满分12分)
讨论函数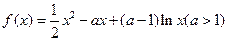 的单调性。
的单调性。
((本小题满分12分)
长方体ABCD—A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直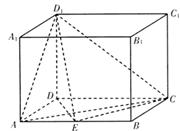
(I)求线段AE的长;
(II)求二面角D1—EC—D的 大小;
大小;
(III)求A点到平面CD1E的距离。
(本小题满分12分)
某校选拔 若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三
若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三 人合格的概率依次为0.5、0.6、0.4,第二次选拔,甲、乙、丙三人合格的概率依次为0.6、0.5、0.5。
人合格的概率依次为0.5、0.6、0.4,第二次选拔,甲、乙、丙三人合格的概率依次为0.6、0.5、0.5。
(I)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(II)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(III)设经过前后两次选拔后合格入选的人数为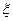 ,求
,求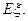
.(本小题满分12 分)
分) 已知向量
已知向量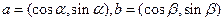 ,且
,且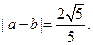
(I)求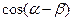 的值;
的值;
(II)若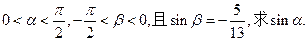
(本小题满分14分)
设函数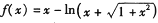 .
.
(I )讨论函数/(均的单调性;
(II)若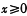 时,恒有
时,恒有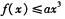 ,试求实数a的取值范围;
,试求实数a的取值范围;
(III)令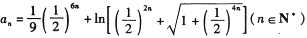 ,试证明:
,试证明: