.设椭圆C: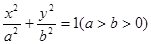 的左焦点为
的左焦点为 ,上顶点为
,上顶点为 ,过点
,过点 作垂直于
作垂直于 直线交椭圆
直线交椭圆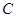 于另外一点
于另外一点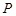 ,交
,交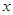 轴正半轴于点
轴正半轴于点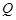 ,
,
且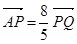
⑴求椭圆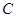 的离心率;
的离心率;
⑵若过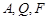 三点的圆恰好与直线
三点的圆恰好与直线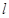
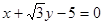 相切,求椭圆C的方程.
相切,求椭圆C的方程. 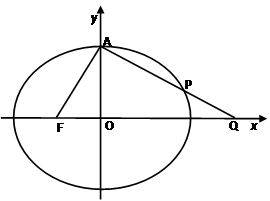
(本小题6分)
如图,矩形 的两条对角线相交于点
的两条对角线相交于点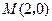 ,
,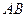 边所在直线的方程为
边所在直线的方程为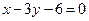 , 点
, 点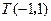 在
在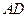 边所在直线上.求:
边所在直线上.求:
(1)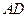 边所在直线的方程;
边所在直线的方程;
(2)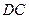 边所在的直线方程.
边所在的直线方程.
(本小题12分)
已知圆C: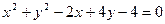 ;
;
(1)若直线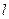 过
过 且与圆C相切,求直线
且与圆C相切,求直线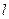 的方程.
的方程.
(2)是否存在斜率为1直线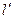 ,使直线
,使直线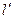 被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
出直线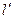 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题10分)
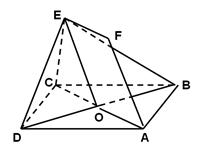
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC.
(1)求证:平面ABFE⊥平面DCFE;
(2)求四面体B—DEF的体积.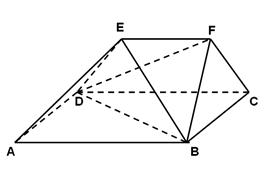
(本小题10分)
已知圆C上一点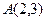 ,直线
,直线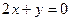 平分圆C,且圆C与直线
平分圆C,且圆C与直线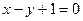 相交的弦长为
相交的弦长为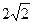 ,
,
求圆C的方程.
(本小题8分)
如图,正方形ABCD和四边形ACEF所在的平面互相垂直. EF//AC,AB=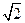 ,CE=EF=1,
,CE=EF=1,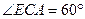 .
.
(1)求证:AF//平面BDE;
(2)求异面直线AB与DE所成角的余弦值.