.(本小题满分14分)已知函数 对任意实数
对任意实数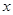 均有
均有 ,当
,当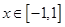 时,
时, 是正比例函数,当
是正比例函数,当 时,
时, 是二次函数,且在
是二次函数,且在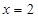 时
时 取最小值
取最小值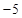 。
。
(1)证明: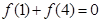 ;
;
(2)求出 在
在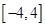 的表达式;并讨论
的表达式;并讨论 在
在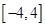 的单调性。
的单调性。
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
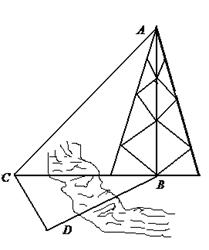
如图,测量河对岸的塔高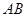 时,可以选与塔底
时,可以选与塔底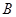 在同一水平面内的两个测点
在同一水平面内的两个测点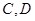 .现测得
.现测得
 ,并在点
,并在点 测得塔顶
测得塔顶 的仰角为
的仰角为 , 求塔高
, 求塔高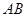 (精确到
(精确到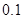 ,
,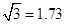 )
)
已知数列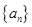 的前
的前 项和为
项和为 ,且
,且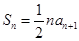 (
( N*),其中
N*),其中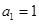 .
.
(Ⅰ) 求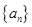 的通项公式;
的通项公式;
(Ⅱ) 设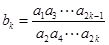 (
( N*).
N*).
①证明:  ;
;
② 求证: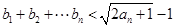 .
.
已知各项都不为零的数列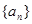 的前n项和为
的前n项和为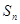 ,
, ,向量
,向量 ,其中
,其中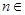 N*,且
N*,且 ∥
∥ .
.
(Ⅰ)求数列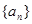 的通项公式及
的通项公式及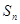 ;
;
(Ⅱ)若数列 的前n项和为
的前n项和为 ,且
,且 (其中
(其中 是首项
是首项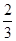 ,第四项为
,第四项为 的等比数列的公比),求证:
的等比数列的公比),求证: .
.
汕头二中拟建一座长 米,宽
米,宽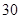 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米(
米(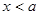 ,
, 为正常数)需打建一个桩位,每个桩位需花费
为正常数)需打建一个桩位,每个桩位需花费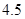 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?