(本题满分14分)已知函数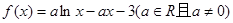 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点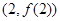 处的切线的倾斜角为
处的切线的倾斜角为 ,问:
,问: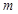 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的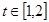 ,函数
,函数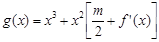 在区间
在区间 上总存在极值?
上总存在极值?
(Ⅲ)当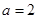 时,设函数
时,设函数 ,若在区间
,若在区间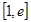 上至少存在一个
上至少存在一个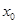 ,使得
,使得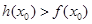 成立,试求实数
成立,试求实数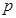 的取值范围.
的取值范围.
设排球队A与B进行比赛,规定若有一队胜四场,则为获胜队,已知两队水平相当
(1)求A队第一、五场输,第二、三、四场赢,最终获胜的概率;
(2)若要决出胜负,平均需要比赛几场?
(1)解关于x的不等式
(2)记a>0时(1)中不等式的解集为A,集合B= ,若
,若 恰有3个元素,求a的取值范围。
恰有3个元素,求a的取值范围。
设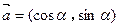 ,
,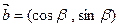
(1)若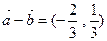 ,
,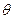 为
为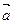 与
与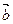 的夹角,求
的夹角,求 。
。
(2)若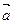 与
与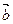 夹角为60o,那么t为何值时
夹角为60o,那么t为何值时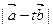 的值最小?
的值最小?
5. 已知数列 ,其中
,其中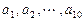 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为 的等差数列;
的等差数列;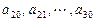 是公差为
是公差为 的等差数列(
的等差数列( ).
).
(1)若 ,求
,求 ;
;
(2)试写出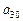 关于
关于 的关系式,并求
的关系式,并求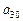 的取值范围;
的取值范围;
(3)续写已知数列,使得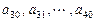 是公差为
是公差为 的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
深夜,一辆出租车被牵涉进一起交通事故,该市有两家出租车公司——红色出租车公司和蓝色出租车公司,其中蓝色出租车公司和红色出租车公司分别占整个城市出租车的85%和15%。据现场目击证人说,事故现场的出租车是红色,并对证人的辨别能力作了测试,测得他辨认的正确率为80%,于是警察就认定红色出租车具有较大的肇事嫌疑. 请问警察的认定对红色出租车公平吗?试说明理由.