5. 已知数列 ,其中
,其中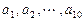 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为 的等差数列;
的等差数列;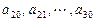 是公差为
是公差为 的等差数列(
的等差数列( ).
).
(1)若 ,求
,求 ;
;
(2)试写出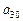 关于
关于 的关系式,并求
的关系式,并求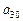 的取值范围;
的取值范围;
(3)续写已知数列,使得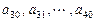 是公差为
是公差为 的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
某次考试中,从甲,乙两个班各抽取10名学生的成绩进行统计分析,两班10名学生成绩的茎叶图如图所示,成绩不小于90分为及格.
(1)从每班抽取的学生中各抽取一人,求至少有一个及格的概率;
(2)从甲班10人中取两人,乙班10人中取一人,三人中及格人数记为X,求X的分布列和数学期望.
某学生参加某高校的自主招生考试,须依次参加A,B,C,D,E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试.已知每一项测试都是相互独立的,该生参加A,B,C,D四项考试不合格的概率均为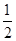 ,参加第五项不合格的概率为
,参加第五项不合格的概率为 .
.
(1)求该生被录取的概率;
(2)记该生参加考试的项数为X,求X的分布列和期望.
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜3次,每次相互独立;
②每次竞猜时,先由甲写出一个数字,记为a,再由乙猜甲写的数字,记为b,已知a,b∈{0,1,2,3,4,5},若|a-b|≤1,则本次竞猜成功;
③在3次竞猜中,至少有2次竞猜成功,则两人获奖.
求甲乙两人玩此游戏获奖的概率.
已知函数f(x)= sin
sin cos
cos +sin2
+sin2 (其中ω>0,0<φ<
(其中ω>0,0<φ<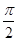 ).其图象的两个相邻对称中心的距离为
).其图象的两个相邻对称中心的距离为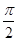 ,且过点
,且过点 .
.
(1)函数f(x)的解析式;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,a= ,S△ABC=2
,S△ABC=2 ,角C为锐角.且满足f
,角C为锐角.且满足f =
=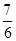 ,求c的值.
,求c的值.
已知m=(2cos x+2 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)将y表示为x的函数f(x),并求f(x)的单调增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.