(本小题满分12分)
已知椭圆 的离心率为
的离心率为 ,且短轴长为2。
,且短轴长为2。
(I)求椭圆方程;
(II)过点(m,0)作圆 的切线交椭圆于A、B两点,试将
的切线交椭圆于A、B两点,试将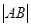 表示为m的函数,并求
表示为m的函数,并求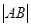 的最大值。
的最大值。
已知
,函数
.
(1)求曲线
在点
处的切线方程;
(2)当
时,求
的最大值.
如图,点
(0,﹣1)是椭圆
:
的一个顶点,
的长轴是圆
:
的直径,
,
是过点
且互相垂直的两条直线,其中
交圆
于
两点,
交椭圆
于另一点
.
(1)求椭圆
的方程;
(2)求
面积的最大值时直线
的方程.
如图,在四面体
中,
平面
,
.
是
的中点,
是
的中点,点
在线段
上,且
.
(1)证明:
平面
;
(2)若二面角
的大小为60°,求
的大小.
设袋子中装有
个红球,
个黄球,
个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分.
(1)当
=3,
=2,
=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
为取出此2球所得分数之和.,求
分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量
为取出此球所得分数.若
,求
:
:
.
在公差为d的等差数列
中,已知
,且
成等比数列.
(1)求
;
(2)若
,求
.