(本小题满分12分)
已知关于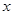 的一元二次函数
的一元二次函数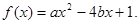
(Ⅰ)设集合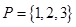 和
和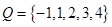 ,分别从集合
,分别从集合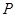 和
和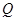 中随
中随 机取一个数作为
机取一个数作为 和
和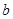 ,求函数
,求函数
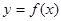 在区间[
在区间[ 上是增函数的概率;
上是增函数的概率;
(Ⅱ)设点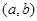 是区域
是区域 内的随机点,
内的随机点,
记 有两个零点,其中一个大于
有两个零点,其中一个大于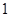 ,另一个小于
,另一个小于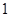
 ,求事件
,求事件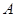 发生的概率.
发生的概率.
已知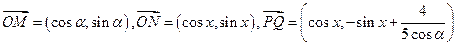
(1)当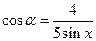 时,求函数
时,求函数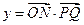 的最小正周期;
的最小正周期;
(2)当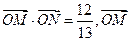 ∥
∥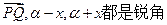 时,求
时,求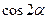 的值.
的值.
已知函数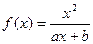 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;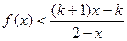
等比数列{an}中a1=8,且bn=log2 an数列{bn}的前n项和为Sn ,且S7≠S8 又S7最大.
①求证:{bn}成等差数列②求数列{an}的公比q的取值范围.
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2DC,F是BE的中点,求证:(1) FD∥平面ABC; (2)FD⊥平面ABE; (3) AF⊥平面EDB.
在△ABC中,角A、B、C的对边分别为a、b、c,且满足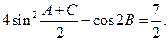
(Ⅰ)求角B的度数;
(Ⅱ)如果b = ,a + c = 3且a>c,求a、c的值.
,a + c = 3且a>c,求a、c的值.